Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 145953 by mathdanisur last updated on 09/Jul/21

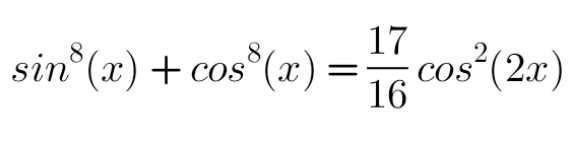
Commented by mathdanisur last updated on 09/Jul/21

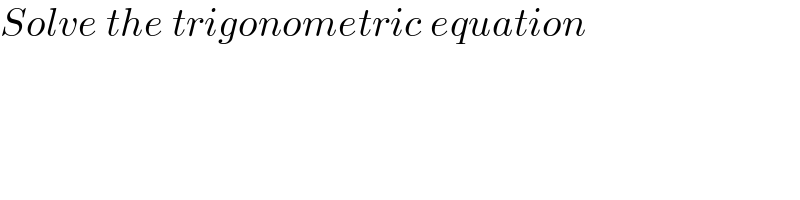
Solve the trigonometric equation

$${Solve}\:{the}\:{trigonometric}\:{equation} \\ $$

Commented by puissant last updated on 09/Jul/21

What do you need?

$$\mathrm{What}\:\mathrm{do}\:\mathrm{you}\:\mathrm{need}? \\ $$

Commented by iloveisrael last updated on 10/Jul/21

Commented by mr W last updated on 10/Jul/21

your solutions are: x=kπ±((3π)/8), x=kπ±(π/8) that means: x=..., −((3π)/8), −(π/8), (π/8), ((3π)/8), ((5π)/8), ((7π)/8), ... this can also be written as x=((kπ)/4)+(π/8)

$${your}\:{solutions}\:{are}: \\ $$$${x}={k}\pi\pm\frac{\mathrm{3}\pi}{\mathrm{8}},\:{x}={k}\pi\pm\frac{\pi}{\mathrm{8}} \\ $$$${that}\:{means}: \\ $$$${x}=...,\:−\frac{\mathrm{3}\pi}{\mathrm{8}},\:−\frac{\pi}{\mathrm{8}},\:\frac{\pi}{\mathrm{8}},\:\frac{\mathrm{3}\pi}{\mathrm{8}},\:\frac{\mathrm{5}\pi}{\mathrm{8}},\:\frac{\mathrm{7}\pi}{\mathrm{8}},\:... \\ $$$${this}\:{can}\:{also}\:{be}\:{written}\:{as} \\ $$$${x}=\frac{{k}\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{8}} \\ $$

Answered by mr W last updated on 09/Jul/21

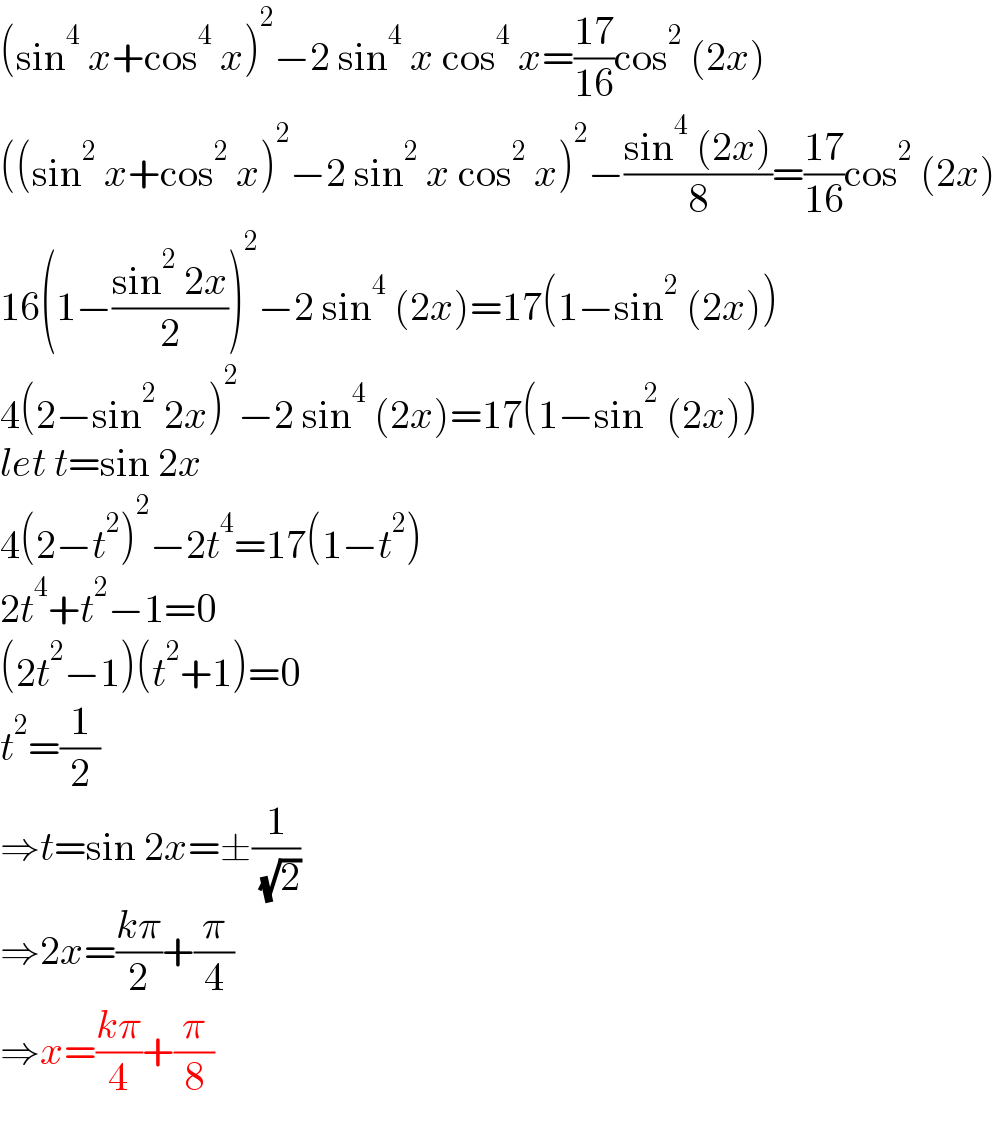
(sin^4 x+cos^4 x)^2 −2 sin^4 x cos^4 x=((17)/(16))cos^2 (2x) ((sin^2 x+cos^2 x)^2 −2 sin^2 x cos^2 x)^2 −((sin^4 (2x))/8)=((17)/(16))cos^2 (2x) 16(1−((sin^2 2x)/2))^2 −2 sin^4 (2x)=17(1−sin^2 (2x)) 4(2−sin^2 2x)^2 −2 sin^4 (2x)=17(1−sin^2 (2x)) let t=sin 2x 4(2−t^2 )^2 −2t^4 =17(1−t^2 ) 2t^4 +t^2 −1=0 (2t^2 −1)(t^2 +1)=0 t^2 =(1/2) ⇒t=sin 2x=±(1/( (√2))) ⇒2x=((kπ)/2)+(π/4) ⇒x=((kπ)/4)+(π/8)

$$\left(\mathrm{sin}^{\mathrm{4}} \:{x}+\mathrm{cos}^{\mathrm{4}} \:{x}\right)^{\mathrm{2}} −\mathrm{2}\:\mathrm{sin}^{\mathrm{4}} \:{x}\:\mathrm{cos}^{\mathrm{4}} \:{x}=\frac{\mathrm{17}}{\mathrm{16}}\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}{x}\right) \\ $$$$\left(\left(\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{x}\right)^{\mathrm{2}} −\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{2}} \:{x}\right)^{\mathrm{2}} −\frac{\mathrm{sin}^{\mathrm{4}} \:\left(\mathrm{2}{x}\right)}{\mathrm{8}}=\frac{\mathrm{17}}{\mathrm{16}}\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}{x}\right) \\ $$$$\mathrm{16}\left(\mathrm{1}−\frac{\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}\:\mathrm{sin}^{\mathrm{4}} \:\left(\mathrm{2}{x}\right)=\mathrm{17}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{2}{x}\right)\right) \\ $$$$\mathrm{4}\left(\mathrm{2}−\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}\right)^{\mathrm{2}} −\mathrm{2}\:\mathrm{sin}^{\mathrm{4}} \:\left(\mathrm{2}{x}\right)=\mathrm{17}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{2}{x}\right)\right) \\ $$$${let}\:{t}=\mathrm{sin}\:\mathrm{2}{x} \\ $$$$\mathrm{4}\left(\mathrm{2}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}{t}^{\mathrm{4}} =\mathrm{17}\left(\mathrm{1}−{t}^{\mathrm{2}} \right) \\ $$$$\mathrm{2}{t}^{\mathrm{4}} +{t}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$${t}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{t}=\mathrm{sin}\:\mathrm{2}{x}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{2}{x}=\frac{{k}\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\frac{{k}\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{8}} \\ $$

Commented by mr W last updated on 10/Jul/21

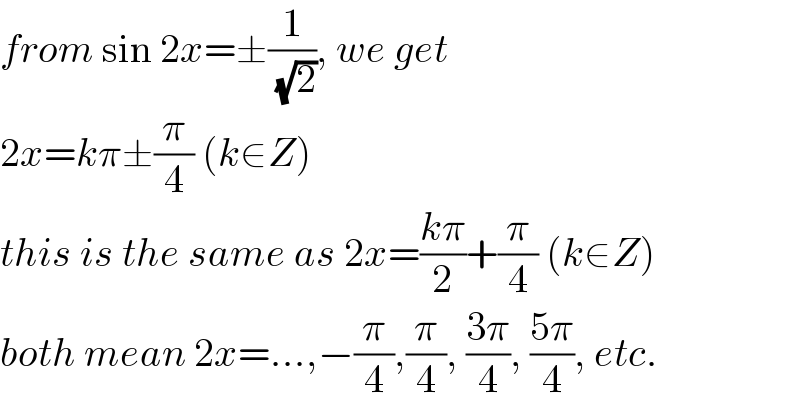
from sin 2x=±(1/( (√2))), we get 2x=kπ±(π/4) (k∈Z) this is the same as 2x=((kπ)/2)+(π/4) (k∈Z) both mean 2x=...,−(π/4),(π/4), ((3π)/4), ((5π)/4), etc.

$${from}\:\mathrm{sin}\:\mathrm{2}{x}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}},\:{we}\:{get} \\ $$$$\mathrm{2}{x}={k}\pi\pm\frac{\pi}{\mathrm{4}}\:\left({k}\in{Z}\right) \\ $$$${this}\:{is}\:{the}\:{same}\:{as}\:\mathrm{2}{x}=\frac{{k}\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\:\left({k}\in{Z}\right) \\ $$$${both}\:{mean}\:\mathrm{2}{x}=...,−\frac{\pi}{\mathrm{4}},\frac{\pi}{\mathrm{4}},\:\frac{\mathrm{3}\pi}{\mathrm{4}},\:\frac{\mathrm{5}\pi}{\mathrm{4}},\:{etc}. \\ $$

Commented by mathdanisur last updated on 09/Jul/21

Cool Ser, thank you

$${Cool}\:{Ser},\:{thank}\:{you} \\ $$

Commented by iloveisrael last updated on 10/Jul/21

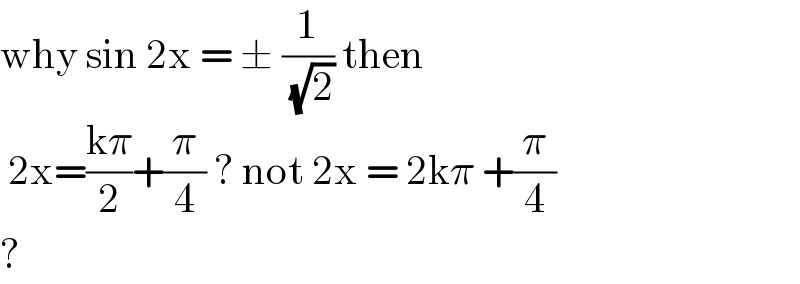
why sin 2x = ± (1/( (√2))) then 2x=((kπ)/2)+(π/4) ? not 2x = 2kπ +(π/4) ?

$$\mathrm{why}\:\mathrm{sin}\:\mathrm{2x}\:=\:\pm\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{then}\: \\ $$$$\:\mathrm{2x}=\frac{\mathrm{k}\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\:?\:\mathrm{not}\:\mathrm{2x}\:=\:\mathrm{2k}\pi\:+\frac{\pi}{\mathrm{4}} \\ $$$$? \\ $$

Commented by iloveisrael last updated on 10/Jul/21

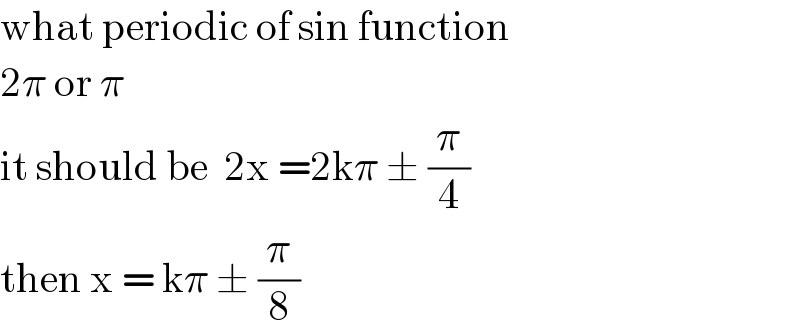
what periodic of sin function 2π or π it should be 2x =2kπ ± (π/4) then x = kπ ± (π/8)

$$\mathrm{what}\:\mathrm{periodic}\:\mathrm{of}\:\mathrm{sin}\:\mathrm{function} \\ $$$$\mathrm{2}\pi\:\mathrm{or}\:\pi\: \\ $$$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\:\mathrm{2x}\:=\mathrm{2k}\pi\:\pm\:\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{then}\:\mathrm{x}\:=\:\mathrm{k}\pi\:\pm\:\frac{\pi}{\mathrm{8}}\: \\ $$

Commented by mr W last updated on 10/Jul/21

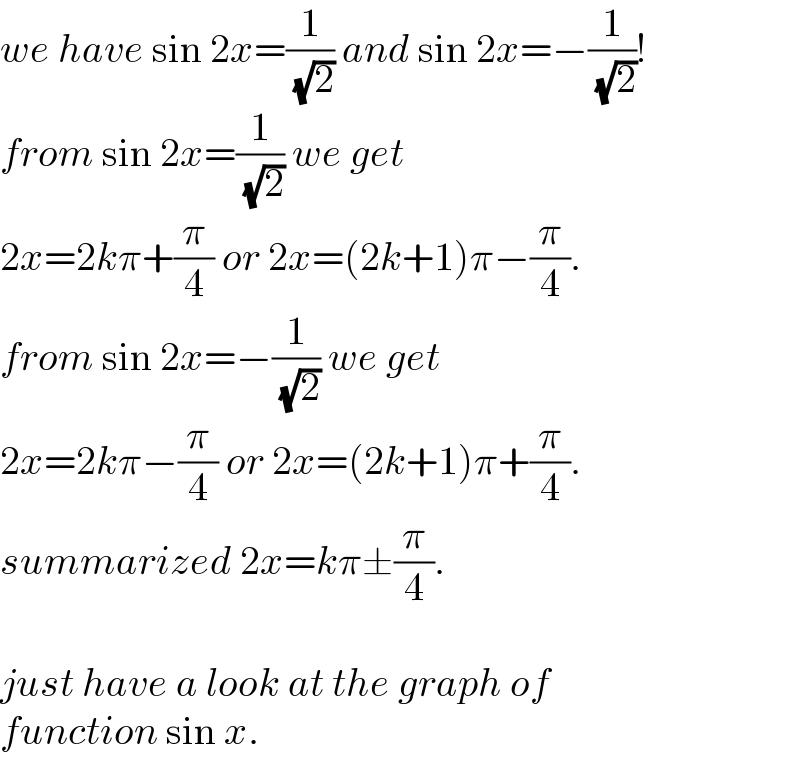
we have sin 2x=(1/( (√2))) and sin 2x=−(1/( (√2)))! from sin 2x=(1/( (√2))) we get 2x=2kπ+(π/4) or 2x=(2k+1)π−(π/4). from sin 2x=−(1/( (√2))) we get 2x=2kπ−(π/4) or 2x=(2k+1)π+(π/4). summarized 2x=kπ±(π/4). just have a look at the graph of function sin x.

$${we}\:{have}\:\mathrm{sin}\:\mathrm{2}{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{and}\:\mathrm{sin}\:\mathrm{2}{x}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}! \\ $$$${from}\:\mathrm{sin}\:\mathrm{2}{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{we}\:{get} \\ $$$$\mathrm{2}{x}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{4}}\:{or}\:\mathrm{2}{x}=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi−\frac{\pi}{\mathrm{4}}. \\ $$$${from}\:\mathrm{sin}\:\mathrm{2}{x}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{we}\:{get} \\ $$$$\mathrm{2}{x}=\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{4}}\:{or}\:\mathrm{2}{x}=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi+\frac{\pi}{\mathrm{4}}. \\ $$$${summarized}\:\mathrm{2}{x}={k}\pi\pm\frac{\pi}{\mathrm{4}}. \\ $$$$ \\ $$$${just}\:{have}\:{a}\:{look}\:{at}\:{the}\:{graph}\:{of} \\ $$$${function}\:\mathrm{sin}\:{x}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com