
Question Number 145947 by Khalmohmmad last updated on 09/Jul/21

Commented by hknkrc46 last updated on 09/Jul/21
![{: ((∫f(x)dx = F(x) + c)),((∫g(x)dx = G(x) + c)) } determinant (((G(2) = 3)),((f(5) = 1))) • f(x) = F ′(x) ∧ g(x) = G ′(x) • ((d[(x^2 + 2)G(x)])/dx) = ((d[F(3x − 1)])/dx) ⇒ 2xG(x) + (x^2 + 2)G ′(x) = 3F ′(3x − 1) ⇒ 2xG(x) + (x^2 + 2)g(x) = 3f(3x − 1) ▶ x = 2 ⇒ 4G(2) + 6g(2) = 3f(5) ⇒ 12 + 6g(2) = 3 ⇒ g(2) = −(3/2)](Q145949.png)
$$\:\left.\begin{matrix}{\int\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}\:=\:\boldsymbol{{F}}\left(\boldsymbol{{x}}\right)\:+\:\boldsymbol{{c}}}\\{\int\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}\:=\:\boldsymbol{{G}}\left(\boldsymbol{{x}}\right)\:+\:\boldsymbol{{c}}}\end{matrix}\right\}\:\begin{matrix}{\boldsymbol{{G}}\left(\mathrm{2}\right)\:=\:\mathrm{3}}\\{\boldsymbol{{f}}\left(\mathrm{5}\right)\:=\:\mathrm{1}}\end{matrix} \\ $$$$ \\ $$$$\:\:\:\bullet\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\:=\:\boldsymbol{{F}}\:'\left(\boldsymbol{{x}}\right)\:\wedge\:\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)\:=\:\boldsymbol{{G}}\:'\left(\boldsymbol{{x}}\right) \\ $$$$\:\:\:\bullet\:\frac{\boldsymbol{{d}}\left[\left(\boldsymbol{{x}}^{\mathrm{2}} \:+\:\mathrm{2}\right)\boldsymbol{{G}}\left(\boldsymbol{{x}}\right)\right]}{\boldsymbol{{dx}}}\:=\:\frac{\boldsymbol{{d}}\left[\boldsymbol{{F}}\left(\mathrm{3}\boldsymbol{{x}}\:−\:\mathrm{1}\right)\right]}{\boldsymbol{{dx}}} \\ $$$$\:\:\:\Rightarrow\:\mathrm{2}\boldsymbol{{xG}}\left(\boldsymbol{{x}}\right)\:+\:\left(\boldsymbol{{x}}^{\mathrm{2}} \:+\:\mathrm{2}\right)\boldsymbol{{G}}\:'\left(\boldsymbol{{x}}\right)\:=\:\mathrm{3}\boldsymbol{{F}}\:'\left(\mathrm{3}\boldsymbol{{x}}\:−\:\mathrm{1}\right) \\ $$$$\:\:\:\Rightarrow\:\mathrm{2}\boldsymbol{{xG}}\left(\boldsymbol{{x}}\right)\:+\:\left(\boldsymbol{{x}}^{\mathrm{2}} \:+\:\mathrm{2}\right)\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)\:=\:\mathrm{3}\boldsymbol{{f}}\left(\mathrm{3}\boldsymbol{{x}}\:−\:\mathrm{1}\right) \\ $$$$\:\:\:\blacktriangleright\:\boldsymbol{{x}}\:=\:\mathrm{2}\:\Rightarrow\:\mathrm{4}\boldsymbol{{G}}\left(\mathrm{2}\right)\:+\:\mathrm{6}\boldsymbol{{g}}\left(\mathrm{2}\right)\:=\:\mathrm{3}\boldsymbol{{f}}\left(\mathrm{5}\right) \\ $$$$\:\:\:\Rightarrow\:\mathrm{12}\:+\:\mathrm{6}\boldsymbol{{g}}\left(\mathrm{2}\right)\:=\:\mathrm{3}\:\Rightarrow\:\boldsymbol{{g}}\left(\mathrm{2}\right)\:=\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by puissant last updated on 09/Jul/21
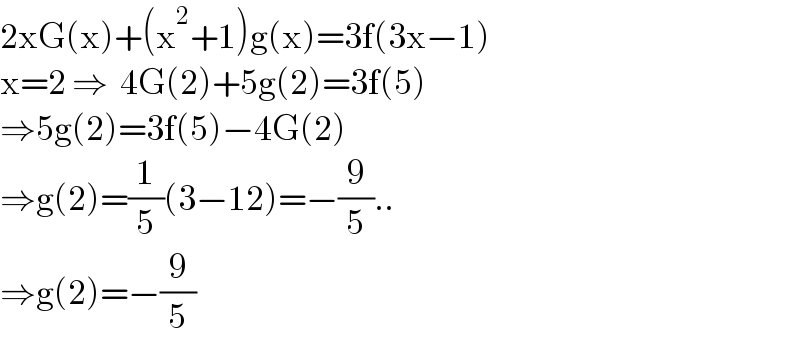
$$\mathrm{2xG}\left(\mathrm{x}\right)+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{g}\left(\mathrm{x}\right)=\mathrm{3f}\left(\mathrm{3x}−\mathrm{1}\right) \\ $$$$\mathrm{x}=\mathrm{2}\:\Rightarrow\:\:\mathrm{4G}\left(\mathrm{2}\right)+\mathrm{5g}\left(\mathrm{2}\right)=\mathrm{3f}\left(\mathrm{5}\right) \\ $$$$\Rightarrow\mathrm{5g}\left(\mathrm{2}\right)=\mathrm{3f}\left(\mathrm{5}\right)−\mathrm{4G}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{3}−\mathrm{12}\right)=−\frac{\mathrm{9}}{\mathrm{5}}.. \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{2}\right)=−\frac{\mathrm{9}}{\mathrm{5}} \\ $$
