
Question Number 145918 by mathdanisur last updated on 09/Jul/21
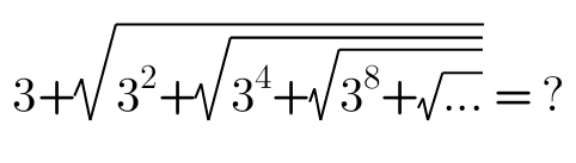
Answered by Olaf_Thorendsen last updated on 09/Jul/21
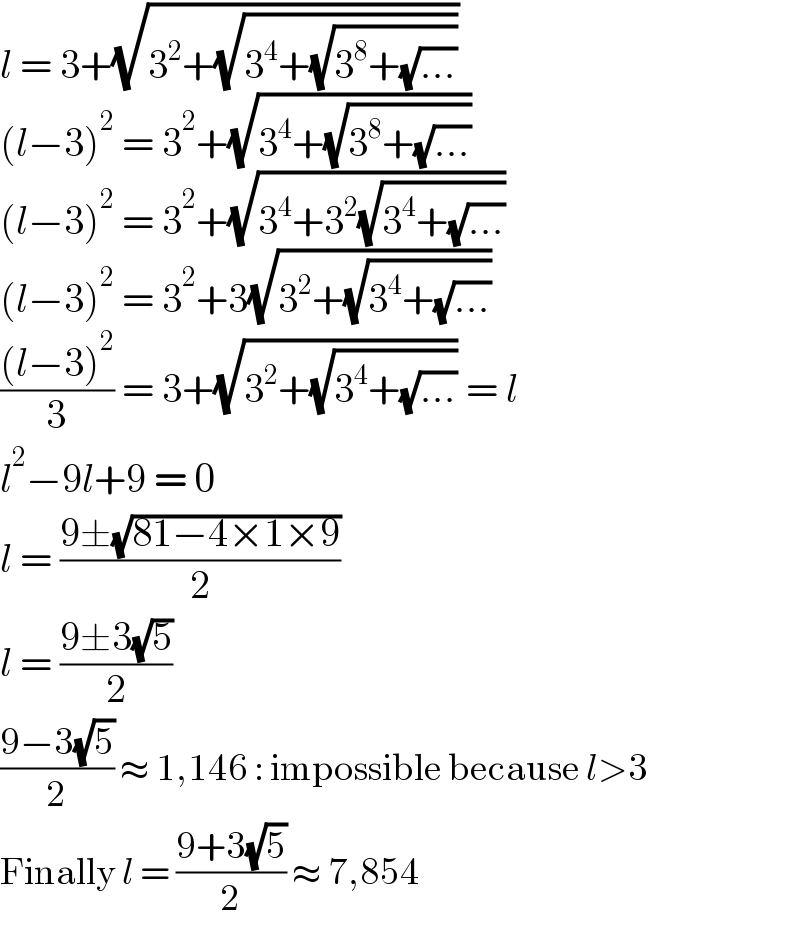
$${l}\:=\:\mathrm{3}+\sqrt{\mathrm{3}^{\mathrm{2}} +\sqrt{\mathrm{3}^{\mathrm{4}} +\sqrt{\mathrm{3}^{\mathrm{8}} +\sqrt{...}}}} \\ $$$$\left({l}−\mathrm{3}\right)^{\mathrm{2}} \:=\:\mathrm{3}^{\mathrm{2}} +\sqrt{\mathrm{3}^{\mathrm{4}} +\sqrt{\mathrm{3}^{\mathrm{8}} +\sqrt{...}}} \\ $$$$\left({l}−\mathrm{3}\right)^{\mathrm{2}} \:=\:\mathrm{3}^{\mathrm{2}} +\sqrt{\mathrm{3}^{\mathrm{4}} +\mathrm{3}^{\mathrm{2}} \sqrt{\mathrm{3}^{\mathrm{4}} +\sqrt{...}}} \\ $$$$\left({l}−\mathrm{3}\right)^{\mathrm{2}} \:=\:\mathrm{3}^{\mathrm{2}} +\mathrm{3}\sqrt{\mathrm{3}^{\mathrm{2}} +\sqrt{\mathrm{3}^{\mathrm{4}} +\sqrt{...}}} \\ $$$$\frac{\left({l}−\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{3}}\:=\:\mathrm{3}+\sqrt{\mathrm{3}^{\mathrm{2}} +\sqrt{\mathrm{3}^{\mathrm{4}} +\sqrt{...}}}\:=\:{l} \\ $$$${l}^{\mathrm{2}} −\mathrm{9}{l}+\mathrm{9}\:=\:\mathrm{0} \\ $$$${l}\:=\:\frac{\mathrm{9}\pm\sqrt{\mathrm{81}−\mathrm{4}×\mathrm{1}×\mathrm{9}}}{\mathrm{2}} \\ $$$${l}\:=\:\frac{\mathrm{9}\pm\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{9}−\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}}\:\approx\:\mathrm{1},\mathrm{146}\::\:\mathrm{impossible}\:\mathrm{because}\:{l}>\mathrm{3} \\ $$$$\mathrm{Finally}\:{l}\:=\:\frac{\mathrm{9}+\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}}\:\approx\:\mathrm{7},\mathrm{854}\: \\ $$
Commented by Mrsof last updated on 09/Jul/21
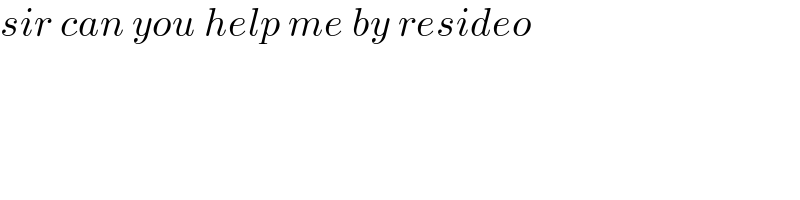
$${sir}\:{can}\:{you}\:{help}\:{me}\:{by}\:{resideo} \\ $$
Commented by Snail last updated on 09/Jul/21
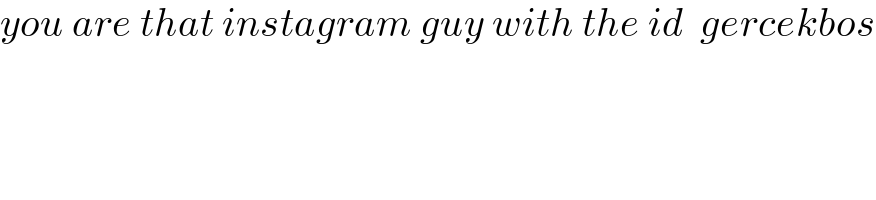
$${you}\:{are}\:{that}\:{instagram}\:{guy}\:{with}\:{the}\:{id}\:\:{gercekbos} \\ $$
Commented by mathdanisur last updated on 09/Jul/21
$${Thankyou}\:{Ser},\:{cool} \\ $$
