Question Number 145483 by ajfour last updated on 05/Jul/21
Commented by ajfour last updated on 05/Jul/21

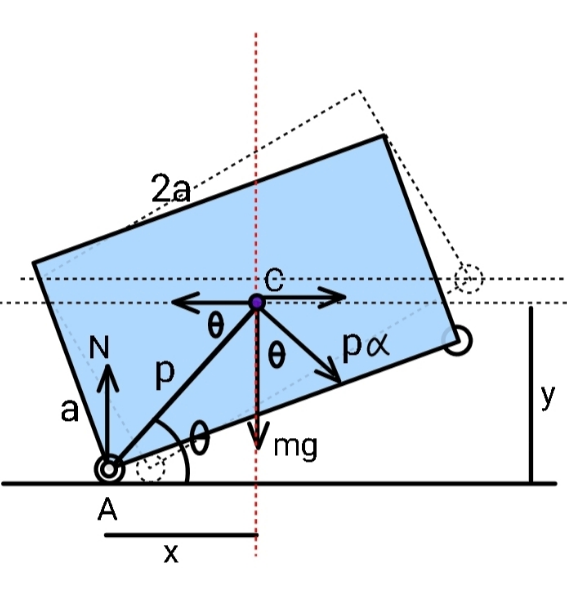
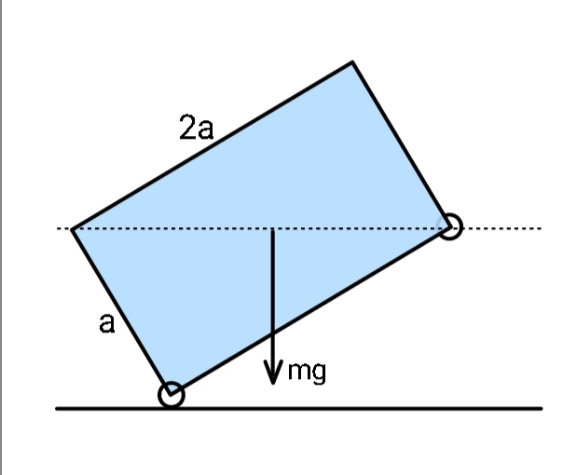
$${If}\:{released}\:{in}\:{this}\:{orientation}, \\ $$$${how}\:{long}\:{shall}\:{it}\:{take}\:{the}\:{other} \\ $$$${wheel}\:{of}\:{the}\:{crate}\:{to}\:{hit}\:{the} \\ $$$${ground}?\:\:\left({no}\:{friction}\:{anywhere}\right) \\ $$
Answered by mr W last updated on 05/Jul/21
Commented by mr W last updated on 06/Jul/21
![AC=p=((√(a^2 +b^2 ))/2) v_x =0 ϕ=tan^(−1) (a/b)=tan^(−1) (1/λ) y_C =p sin (θ+ϕ) v=(dy_C /dt)=pω cos (θ+ϕ) (1/2)mv^2 +(1/2)Iω^2 =mg(((ab)/( (√(a^2 +b^2 ))))−p sin (θ+ϕ)) [1+3 cos^2 (θ+ϕ)]ω^2 =((12g)/( (√(a^2 +b^2 ))))(((2ab)/( a^2 +b^2 ))−sin (θ+ϕ)) let λ=(b/a) [1+3 cos^2 (θ+ϕ)]ω^2 =((12g)/( a(√(1+λ^2 ))))(((2λ)/( 1+λ^2 ))−sin (θ+ϕ)) ω=(dθ/dt)=(√((12g)/(a(√(1+λ^2 )))))×(√((((2λ)/( 1+λ^2 ))−sin (θ+ϕ))/(1+3 cos^2 (θ+ϕ)))) ⇒t=(√((a(√(1+λ^2 )))/(12g)))∫_0 ^ϕ (√((1+3 cos^2 (θ+ϕ))/(((2λ)/( 1+λ^2 ))−sin (θ+ϕ))))dθ ⇒t=(√((a(√(1+λ^2 )))/(12g)))∫_ϕ ^(2ϕ) (√((1+3 cos^2 φ)/(((2λ)/( 1+λ^2 ))−sin φ)))dφ with b=2a, λ=2: ⇒t=(√(((√5)a)/(12g)))∫_(tan^(−1) (1/2)) ^(2tan^(−1) (1/2)) (√((1+3 cos^2 φ)/((4/( 5))−sin φ)))dφ ≈1.149799(√(a/g))](Q145550.png)
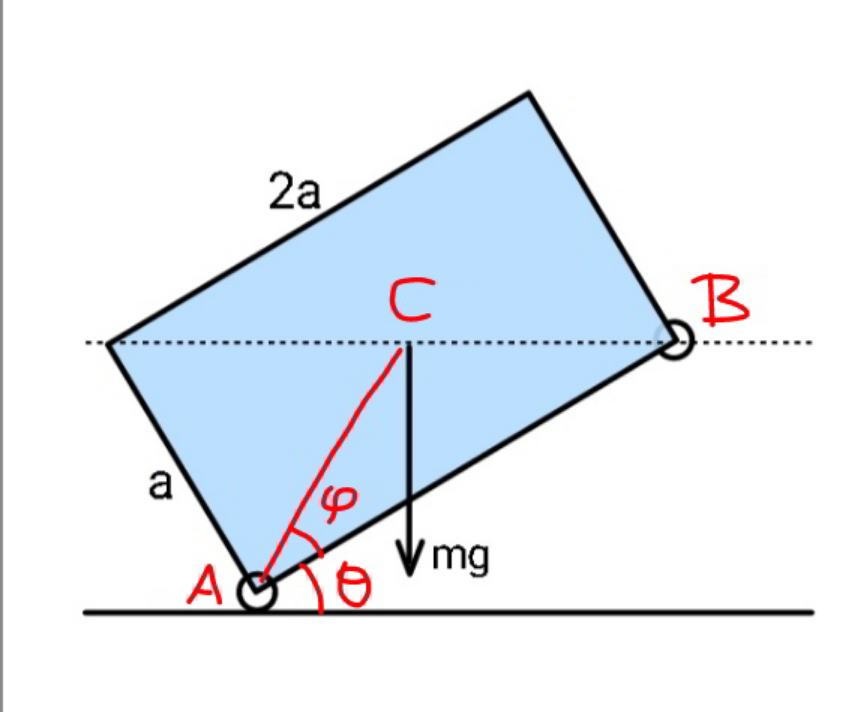
$${AC}={p}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${v}_{{x}} =\mathrm{0} \\ $$$$\varphi=\mathrm{tan}^{−\mathrm{1}} \frac{{a}}{{b}}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\lambda} \\ $$$${y}_{{C}} ={p}\:\mathrm{sin}\:\left(\theta+\varphi\right) \\ $$$${v}=\frac{{dy}_{{C}} }{{dt}}={p}\omega\:\mathrm{cos}\:\left(\theta+\varphi\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} ={mg}\left(\frac{{ab}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}−{p}\:\mathrm{sin}\:\left(\theta+\varphi\right)\right) \\ $$$$\left[\mathrm{1}+\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta+\varphi\right)\right]\omega^{\mathrm{2}} =\frac{\mathrm{12}{g}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\left(\frac{\mathrm{2}{ab}}{\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−\mathrm{sin}\:\left(\theta+\varphi\right)\right) \\ $$$${let}\:\lambda=\frac{{b}}{{a}} \\ $$$$\left[\mathrm{1}+\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta+\varphi\right)\right]\omega^{\mathrm{2}} =\frac{\mathrm{12}{g}}{\:{a}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}\left(\frac{\mathrm{2}\lambda}{\:\mathrm{1}+\lambda^{\mathrm{2}} }−\mathrm{sin}\:\left(\theta+\varphi\right)\right) \\ $$$$ \\ $$$$\omega=\frac{{d}\theta}{{dt}}=\sqrt{\frac{\mathrm{12}{g}}{{a}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}}×\sqrt{\frac{\frac{\mathrm{2}\lambda}{\:\mathrm{1}+\lambda^{\mathrm{2}} }−\mathrm{sin}\:\left(\theta+\varphi\right)}{\mathrm{1}+\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta+\varphi\right)}} \\ $$$$\Rightarrow{t}=\sqrt{\frac{{a}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\mathrm{12}{g}}}\int_{\mathrm{0}} ^{\varphi} \sqrt{\frac{\mathrm{1}+\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta+\varphi\right)}{\frac{\mathrm{2}\lambda}{\:\mathrm{1}+\lambda^{\mathrm{2}} }−\mathrm{sin}\:\left(\theta+\varphi\right)}}{d}\theta \\ $$$$\Rightarrow{t}=\sqrt{\frac{{a}\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}{\mathrm{12}{g}}}\int_{\varphi} ^{\mathrm{2}\varphi} \sqrt{\frac{\mathrm{1}+\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\phi}{\frac{\mathrm{2}\lambda}{\:\mathrm{1}+\lambda^{\mathrm{2}} }−\mathrm{sin}\:\phi}}{d}\phi \\ $$$${with}\:{b}=\mathrm{2}{a},\:\lambda=\mathrm{2}: \\ $$$$\Rightarrow{t}=\sqrt{\frac{\sqrt{\mathrm{5}}{a}}{\mathrm{12}{g}}}\int_{\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\frac{\mathrm{1}+\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\phi}{\frac{\mathrm{4}}{\:\mathrm{5}}−\mathrm{sin}\:\phi}}{d}\phi \\ $$$$\:\:\:\:\:\:\approx\mathrm{1}.\mathrm{149799}\sqrt{\frac{{a}}{{g}}} \\ $$
Commented by ajfour last updated on 06/Jul/21
$${yes},\:{sir},\:{i}\:{was}\:{mistaken},\:{thanks}. \\ $$
Commented by mr W last updated on 06/Jul/21
$${i}\:{can}\:{solve}\:{the}\:{integral}\:{only} \\ $$$${numerically}. \\ $$
Commented by mr W last updated on 06/Jul/21
Commented by ajfour last updated on 06/Jul/21
Thanks for the solution, too; impeccable!
Commented by mr W last updated on 06/Jul/21
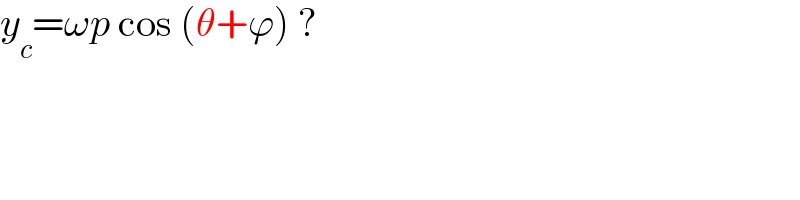
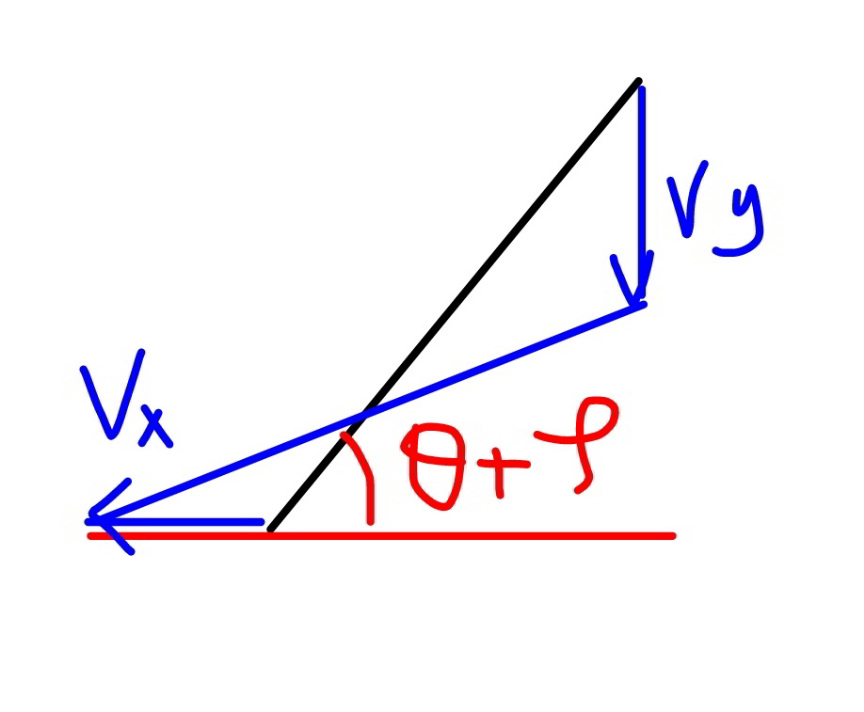
$${y}_{{c}} =\omega{p}\:\mathrm{cos}\:\left(\theta+\varphi\right)\:? \\ $$
Answered by ajfour last updated on 06/Jul/21