Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 145193 by mr W last updated on 03/Jul/21

Commented by mr W last updated on 03/Jul/21

an uniform rod is released horizontally at height h over the top of a tall wall. find the position where the rod strikes the wall for the second time if this happens.

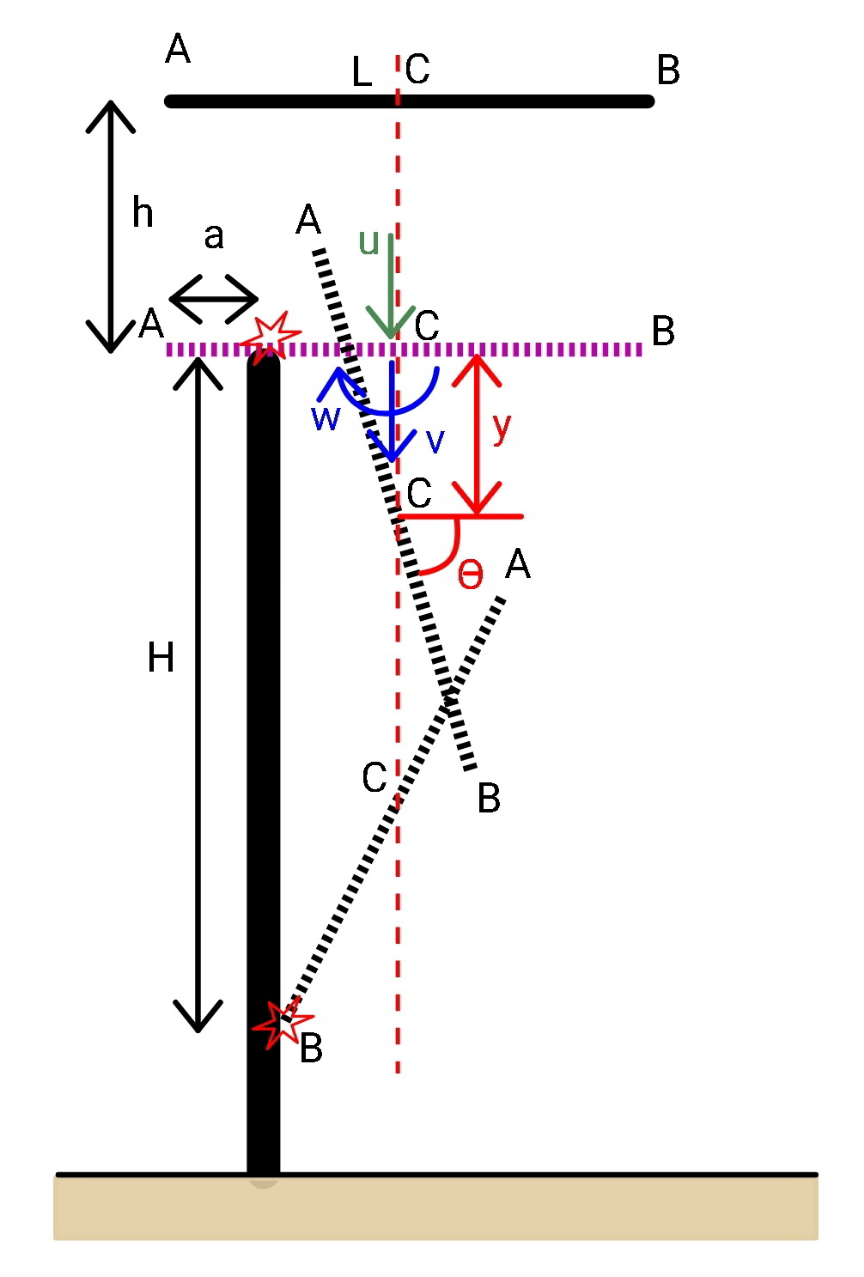
$${an}\:{uniform}\:{rod}\:{is}\:{released}\:{horizontally} \\ $$$${at}\:{height}\:{h}\:{over}\:{the}\:{top}\:{of}\:{a}\:{tall}\:{wall}. \\ $$$${find}\:{the}\:{position}\:{where}\:{the}\:{rod} \\ $$$${strikes}\:{the}\:{wall}\:{for}\:{the}\:{second}\:{time} \\ $$$${if}\:{this}\:{happens}. \\ $$

Answered by mr W last updated on 04/Jul/21

Commented by mr W last updated on 04/Jul/21

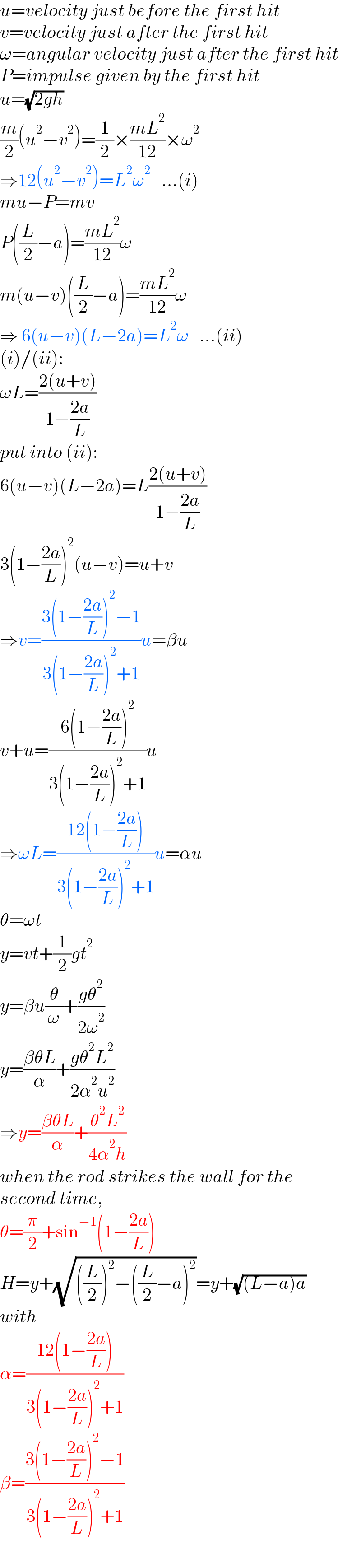
u=velocity just before the first hit v=velocity just after the first hit ω=angular velocity just after the first hit P=impulse given by the first hit u=(√(2gh)) (m/2)(u^2 −v^2 )=(1/2)×((mL^2 )/(12))×ω^2 ⇒12(u^2 −v^2 )=L^2 ω^2 ...(i) mu−P=mv P((L/2)−a)=((mL^2 )/(12))ω m(u−v)((L/2)−a)=((mL^2 )/(12))ω ⇒ 6(u−v)(L−2a)=L^2 ω ...(ii) (i)/(ii): ωL=((2(u+v))/(1−((2a)/L))) put into (ii): 6(u−v)(L−2a)=L((2(u+v))/(1−((2a)/L))) 3(1−((2a)/L))^2 (u−v)=u+v ⇒v=((3(1−((2a)/L))^2 −1)/(3(1−((2a)/L))^2 +1))u=βu v+u=((6(1−((2a)/L))^2 )/(3(1−((2a)/L))^2 +1))u ⇒ωL=((12(1−((2a)/L)))/(3(1−((2a)/L))^2 +1))u=αu θ=ωt y=vt+(1/2)gt^2 y=βu(θ/ω)+((gθ^2 )/(2ω^2 )) y=((βθL)/α)+((gθ^2 L^2 )/(2α^2 u^2 )) ⇒y=((βθL)/α)+((θ^2 L^2 )/(4α^2 h)) when the rod strikes the wall for the second time, θ=(π/2)+sin^(−1) (1−((2a)/L)) H=y+(√(((L/2))^2 −((L/2)−a)^2 ))=y+(√((L−a)a)) with α=((12(1−((2a)/L)))/(3(1−((2a)/L))^2 +1)) β=((3(1−((2a)/L))^2 −1)/(3(1−((2a)/L))^2 +1))

$${u}={velocity}\:{just}\:{before}\:{the}\:{first}\:{hit} \\ $$$${v}={velocity}\:{just}\:{after}\:{the}\:{first}\:{hit} \\ $$$$\omega={angular}\:{velocity}\:{just}\:{after}\:{the}\:{first}\:{hit} \\ $$$${P}={impulse}\:{given}\:{by}\:{the}\:{first}\:{hit} \\ $$$${u}=\sqrt{\mathrm{2}{gh}} \\ $$$$\frac{{m}}{\mathrm{2}}\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{mL}^{\mathrm{2}} }{\mathrm{12}}×\omega^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{12}\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)={L}^{\mathrm{2}} \omega^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$${mu}−{P}={mv} \\ $$$${P}\left(\frac{{L}}{\mathrm{2}}−{a}\right)=\frac{{mL}^{\mathrm{2}} }{\mathrm{12}}\omega \\ $$$${m}\left({u}−{v}\right)\left(\frac{{L}}{\mathrm{2}}−{a}\right)=\frac{{mL}^{\mathrm{2}} }{\mathrm{12}}\omega \\ $$$$\Rightarrow\:\mathrm{6}\left({u}−{v}\right)\left({L}−\mathrm{2}{a}\right)={L}^{\mathrm{2}} \omega\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)/\left({ii}\right): \\ $$$$\omega{L}=\frac{\mathrm{2}\left({u}+{v}\right)}{\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}} \\ $$$${put}\:{into}\:\left({ii}\right): \\ $$$$\mathrm{6}\left({u}−{v}\right)\left({L}−\mathrm{2}{a}\right)={L}\frac{\mathrm{2}\left({u}+{v}\right)}{\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}} \\ $$$$\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)^{\mathrm{2}} \left({u}−{v}\right)={u}+{v} \\ $$$$\Rightarrow{v}=\frac{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)^{\mathrm{2}} +\mathrm{1}}{u}=\beta{u} \\ $$$${v}+{u}=\frac{\mathrm{6}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)^{\mathrm{2}} +\mathrm{1}}{u} \\ $$$$\Rightarrow\omega{L}=\frac{\mathrm{12}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)}{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)^{\mathrm{2}} +\mathrm{1}}{u}=\alpha{u} \\ $$$$\theta=\omega{t} \\ $$$${y}={vt}+\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$${y}=\beta{u}\frac{\theta}{\omega}+\frac{{g}\theta^{\mathrm{2}} }{\mathrm{2}\omega^{\mathrm{2}} } \\ $$$${y}=\frac{\beta\theta{L}}{\alpha}+\frac{{g}\theta^{\mathrm{2}} {L}^{\mathrm{2}} }{\mathrm{2}\alpha^{\mathrm{2}} {u}^{\mathrm{2}} } \\ $$$$\Rightarrow{y}=\frac{\beta\theta{L}}{\alpha}+\frac{\theta^{\mathrm{2}} {L}^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} {h}} \\ $$$${when}\:{the}\:{rod}\:{strikes}\:{the}\:{wall}\:{for}\:{the} \\ $$$${second}\:{time}, \\ $$$$\theta=\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right) \\ $$$${H}={y}+\sqrt{\left(\frac{{L}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{{L}}{\mathrm{2}}−{a}\right)^{\mathrm{2}} }={y}+\sqrt{\left({L}−{a}\right){a}} \\ $$$${with}\: \\ $$$$\alpha=\frac{\mathrm{12}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)}{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\beta=\frac{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{2}{a}}{{L}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com