Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 145166 by tabata last updated on 02/Jul/21

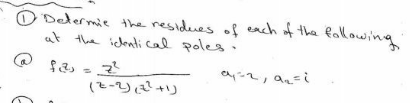
Commented by tabata last updated on 02/Jul/21

help me sir

$${help}\:{me}\:{sir} \\ $$

Answered by mathmax by abdo last updated on 03/Jul/21

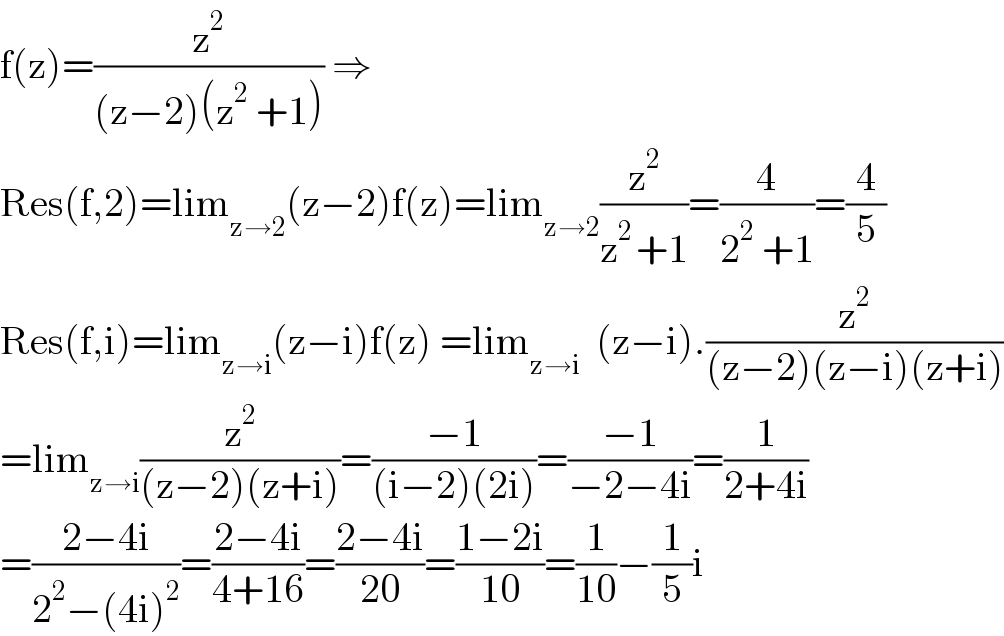
f(z)=(z^2 /((z−2)(z^2 +1))) ⇒ Res(f,2)=lim_(z→2) (z−2)f(z)=lim_(z→2) (z^2 /(z^(2 ) +1))=(4/(2^2 +1))=(4/5) Res(f,i)=lim_(z→i) (z−i)f(z) =lim_(z→i) (z−i).(z^2 /((z−2)(z−i)(z+i))) =lim_(z→i) (z^2 /((z−2)(z+i)))=((−1)/((i−2)(2i)))=((−1)/(−2−4i))=(1/(2+4i)) =((2−4i)/(2^2 −(4i)^2 ))=((2−4i)/(4+16))=((2−4i)/(20))=((1−2i)/(10))=(1/(10))−(1/5)i

$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\mathrm{2}\right)\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{2}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{2}} \left(\mathrm{z}−\mathrm{2}\right)\mathrm{f}\left(\mathrm{z}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{2}} \frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{z}^{\mathrm{2}\:} +\mathrm{1}}=\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{2}} \:+\mathrm{1}}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \left(\mathrm{z}−\mathrm{i}\right)\mathrm{f}\left(\mathrm{z}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\left(\mathrm{z}−\mathrm{i}\right).\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\mathrm{2}\right)\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\mathrm{2}\right)\left(\mathrm{z}+\mathrm{i}\right)}=\frac{−\mathrm{1}}{\left(\mathrm{i}−\mathrm{2}\right)\left(\mathrm{2i}\right)}=\frac{−\mathrm{1}}{−\mathrm{2}−\mathrm{4i}}=\frac{\mathrm{1}}{\mathrm{2}+\mathrm{4i}} \\ $$$$=\frac{\mathrm{2}−\mathrm{4i}}{\mathrm{2}^{\mathrm{2}} −\left(\mathrm{4i}\right)^{\mathrm{2}} }=\frac{\mathrm{2}−\mathrm{4i}}{\mathrm{4}+\mathrm{16}}=\frac{\mathrm{2}−\mathrm{4i}}{\mathrm{20}}=\frac{\mathrm{1}−\mathrm{2i}}{\mathrm{10}}=\frac{\mathrm{1}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{i} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com