
Question Number 144446 by mathdanisur last updated on 25/Jun/21
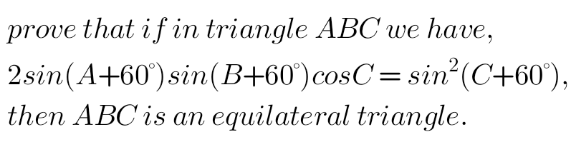
Answered by Rasheed.Sindhi last updated on 26/Jun/21
![2sin(A+60)sin(B+60)cosC =sin^2 (C+60) A=180−(B+C) sin(A+60)=sin( 180−(B+C) ) =sin180cos(B+C)−cos180sin(B+C) =0.cos(B+C)−(−1).sin(B+C) =sin(B+C) 2sin(B+C)sin(B+60)cosC =sin^2 (C+60) ^• sin(B+60) =sinBcos60+cosBsin60 =((1/2))sinB+(((√3)/2))cosB =((sinB+(√3)cosB)/2) ^• sin(C+60)=((sinC+(√3)cosC)/2) RHS: sin^2 (C+60)=[((sinC+(√3)cosC)/2)]^2 =((sin^2 C+3cos^2 C+2(√3)sinCcosC)/4) Let C=60 =(((((√3)/2))^2 +3((1/2))^2 +2(√3)(((√3)/2))((1/2)))/4) =(((3/4)+(3/4)+(3/2))/4)=((12)/(16))=(3/4) LHS: 2sin(B+C)sin(B+60)cosC =2[(sinBcosC+cosBsinC) ×(((sinB+(√3)cosB)/2))cosC] =(sinBcosC+cosBsinC) ×(sinB+(√3)cosB)cosC =(sin60cos60+cos60sin60) ×(sin60+(√3)cos60)cos60 =(((√3)/2).(1/2)+(1/2).((√3)/2))(((√3)/2)+(√3).(1/2))((1/2)) =((√3)/2).(√3).(1/2)=(3/4) ∵ A=B=C=60 ∴ △ABC is an equilateral triangle.](Q144587.png)
$$\mathrm{2}{sin}\left({A}+\mathrm{60}\right){sin}\left({B}+\mathrm{60}\right){cosC} \\ $$$$\:\:\:\:\:\:\:\:={sin}^{\mathrm{2}} \left({C}+\mathrm{60}\right) \\ $$$${A}=\mathrm{180}−\left({B}+{C}\right) \\ $$$${sin}\left({A}+\mathrm{60}\right)={sin}\left(\:\mathrm{180}−\left({B}+{C}\right)\:\right) \\ $$$$\:\:={sin}\mathrm{180}{cos}\left({B}+{C}\right)−{cos}\mathrm{180}{sin}\left({B}+{C}\right) \\ $$$$\:\:=\mathrm{0}.{cos}\left({B}+{C}\right)−\left(−\mathrm{1}\right).{sin}\left({B}+{C}\right) \\ $$$$\:\:={sin}\left({B}+{C}\right) \\ $$$$\mathrm{2}{sin}\left({B}+{C}\right){sin}\left({B}+\mathrm{60}\right){cosC} \\ $$$$\:\:\:\:\:\:\:\:={sin}^{\mathrm{2}} \left({C}+\mathrm{60}\right) \\ $$$$\:^{\bullet} {sin}\left({B}+\mathrm{60}\right) \\ $$$$\:\:\:\:\:\:={sinBcos}\mathrm{60}+{cosBsin}\mathrm{60} \\ $$$$\:\:\:\:\:\:=\left(\frac{\mathrm{1}}{\mathrm{2}}\right){sinB}+\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right){cosB} \\ $$$$\:\:\:\:\:=\frac{{sinB}+\sqrt{\mathrm{3}}{cosB}}{\mathrm{2}} \\ $$$$\:^{\bullet} {sin}\left({C}+\mathrm{60}\right)=\frac{{sinC}+\sqrt{\mathrm{3}}{cosC}}{\mathrm{2}} \\ $$$${RHS}: \\ $$$$\:{sin}^{\mathrm{2}} \left({C}+\mathrm{60}\right)=\left[\frac{{sinC}+\sqrt{\mathrm{3}}{cosC}}{\mathrm{2}}\right]^{\mathrm{2}} \\ $$$$=\frac{{sin}^{\mathrm{2}} {C}+\mathrm{3}{cos}^{\mathrm{2}} {C}+\mathrm{2}\sqrt{\mathrm{3}}{sinCcosC}}{\mathrm{4}} \\ $$$${Let}\:{C}=\mathrm{60} \\ $$$$=\frac{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{4}} \\ $$$$=\frac{\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{2}}}{\mathrm{4}}=\frac{\mathrm{12}}{\mathrm{16}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\:\: \\ $$$${LHS}: \\ $$$$\:\mathrm{2}{sin}\left({B}+{C}\right){sin}\left({B}+\mathrm{60}\right){cosC}\:\:\: \\ $$$$=\mathrm{2}\left[\left({sinBcosC}+{cosBsinC}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:×\left(\frac{{sinB}+\sqrt{\mathrm{3}}{cosB}}{\mathrm{2}}\right){cosC}\right] \\ $$$$=\left({sinBcosC}+{cosBsinC}\right) \\ $$$$\:\:\:\:\:\:\:\:×\left({sinB}+\sqrt{\mathrm{3}}{cosB}\right){cosC} \\ $$$$=\left({sin}\mathrm{60}{cos}\mathrm{60}+{cos}\mathrm{60}{sin}\mathrm{60}\right) \\ $$$$\:\:\:\:\:\:\:\:×\left({sin}\mathrm{60}+\sqrt{\mathrm{3}}{cos}\mathrm{60}\right){cos}\mathrm{60} \\ $$$$=\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\sqrt{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\sqrt{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\because\:{A}={B}={C}=\mathrm{60} \\ $$$$\therefore\:\bigtriangleup{ABC}\:{is}\:{an}\:{equilateral}\:{triangle}. \\ $$$$ \\ $$
Commented by mathdanisur last updated on 26/Jun/21
$${Perfect}\:{thanks}\:{Sir} \\ $$
Answered by Rasheed.Sindhi last updated on 26/Jun/21
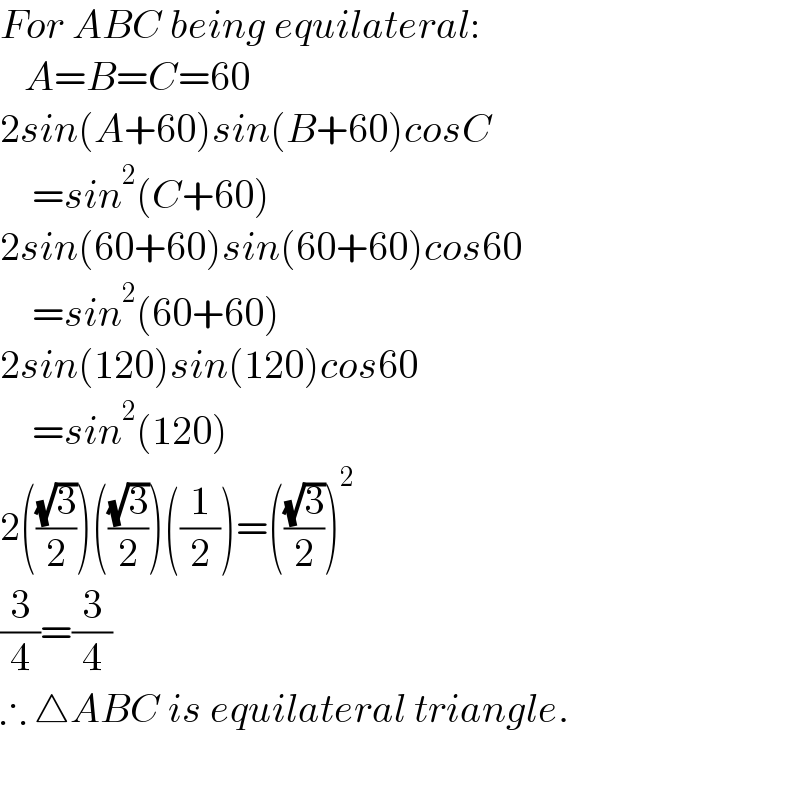
$${For}\:{ABC}\:{being}\:{equilateral}: \\ $$$$\:\:\:{A}={B}={C}=\mathrm{60} \\ $$$$\mathrm{2}{sin}\left({A}+\mathrm{60}\right){sin}\left({B}+\mathrm{60}\right){cosC} \\ $$$$\:\:\:\:={sin}^{\mathrm{2}} \left({C}+\mathrm{60}\right) \\ $$$$\mathrm{2}{sin}\left(\mathrm{60}+\mathrm{60}\right){sin}\left(\mathrm{60}+\mathrm{60}\right){cos}\mathrm{60} \\ $$$$\:\:\:\:={sin}^{\mathrm{2}} \left(\mathrm{60}+\mathrm{60}\right) \\ $$$$\mathrm{2}{sin}\left(\mathrm{120}\right){sin}\left(\mathrm{120}\right){cos}\mathrm{60} \\ $$$$\:\:\:\:={sin}^{\mathrm{2}} \left(\mathrm{120}\right) \\ $$$$\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\therefore\:\bigtriangleup{ABC}\:{is}\:{equilateral}\:{triangle}. \\ $$$$ \\ $$
