
Question Number 144031 by mathdanisur last updated on 20/Jun/21
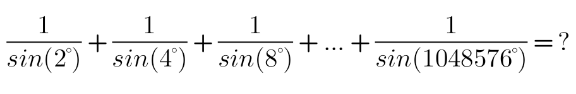
Answered by mindispower last updated on 20/Jun/21
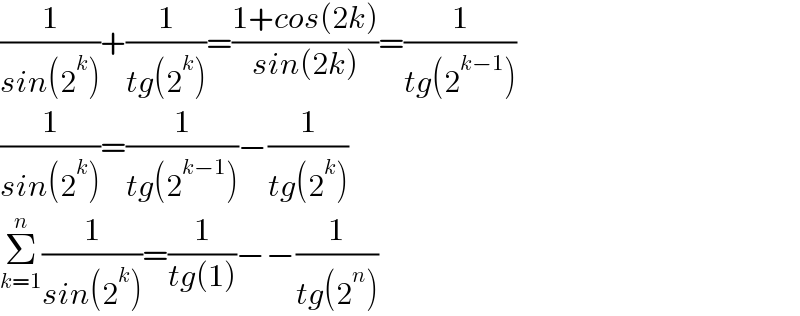
$$\frac{\mathrm{1}}{{sin}\left(\mathrm{2}^{{k}} \right)}+\frac{\mathrm{1}}{{tg}\left(\mathrm{2}^{{k}} \right)}=\frac{\mathrm{1}+{cos}\left(\mathrm{2}{k}\right)}{{sin}\left(\mathrm{2}{k}\right)}=\frac{\mathrm{1}}{{tg}\left(\mathrm{2}^{{k}−\mathrm{1}} \right)} \\ $$$$\frac{\mathrm{1}}{{sin}\left(\mathrm{2}^{{k}} \right)}=\frac{\mathrm{1}}{{tg}\left(\mathrm{2}^{{k}−\mathrm{1}} \right)}−\frac{\mathrm{1}}{{tg}\left(\mathrm{2}^{{k}} \right)} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{sin}\left(\mathrm{2}^{{k}} \right)}=\frac{\mathrm{1}}{{tg}\left(\mathrm{1}\right)}−−\frac{\mathrm{1}}{{tg}\left(\mathrm{2}^{{n}} \right)} \\ $$
Commented by mathdanisur last updated on 22/Jun/21

$${Thanks}\:{Sir}\:{cool} \\ $$
