
Previous in Relation and Functions Next in Relation and Functions
Question Number 144001 by mnjuly1970 last updated on 20/Jun/21
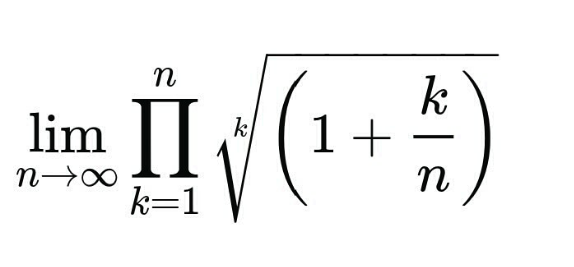
Answered by Dwaipayan Shikari last updated on 20/Jun/21
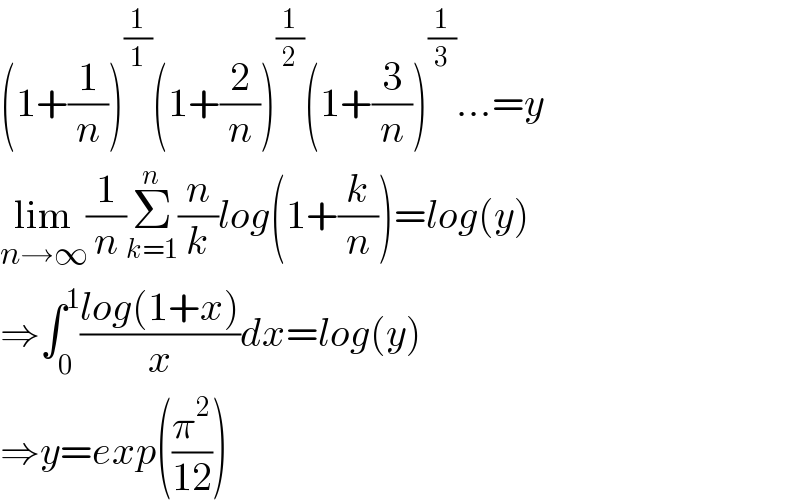
$$\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\frac{\mathrm{1}}{\mathrm{1}}} \left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ...={y} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{n}}{{k}}{log}\left(\mathrm{1}+\frac{{k}}{{n}}\right)={log}\left({y}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{x}\right)}{{x}}{dx}={log}\left({y}\right) \\ $$$$\Rightarrow{y}={exp}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\right) \\ $$
Commented by mnjuly1970 last updated on 20/Jun/21

$$\:{thanks}\:{alot}\:{mr}\:{payan}... \\ $$
Answered by abdullahoudou last updated on 20/Jun/21

$${e}^{\pi^{\mathrm{2}} /\mathrm{12}} \\ $$
Commented by mnjuly1970 last updated on 20/Jun/21
$${tashakor}\:{master}.. \\ $$
