
Question Number 143709 by mnjuly1970 last updated on 17/Jun/21
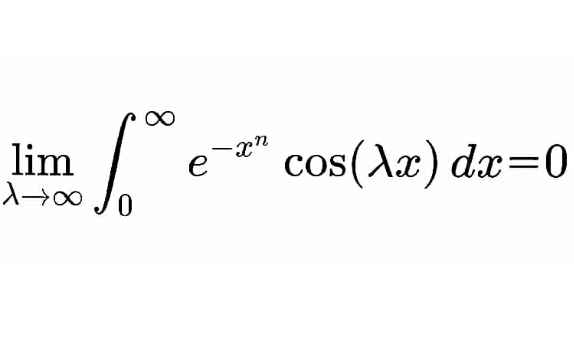
Commented by mnjuly1970 last updated on 17/Jun/21

$$\:\:\:\:{P}\:{rove}\:::\Uparrow\Uparrow\Uparrow \\ $$
Commented by TheHoneyCat last updated on 17/Jun/21
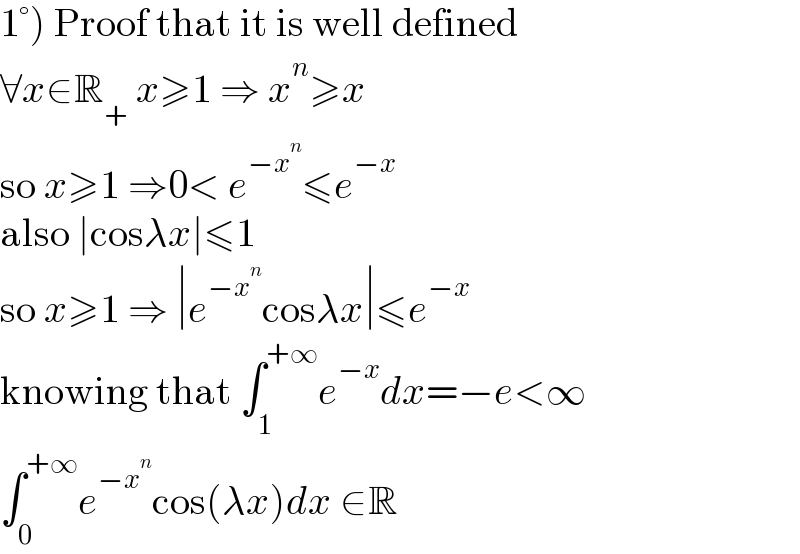
$$\left.\mathrm{1}°\right)\:\mathrm{Proof}\:\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{well}\:\mathrm{defined} \\ $$$$\forall{x}\in\mathbb{R}_{+} \:{x}\geqslant\mathrm{1}\:\Rightarrow\:{x}^{{n}} \geqslant{x} \\ $$$$\mathrm{so}\:{x}\geqslant\mathrm{1}\:\Rightarrow\mathrm{0}<\:{e}^{−{x}^{{n}} } \leqslant{e}^{−{x}} \\ $$$$\mathrm{also}\:\mid\mathrm{cos}\lambda{x}\mid\leqslant\mathrm{1} \\ $$$$\mathrm{so}\:{x}\geqslant\mathrm{1}\:\Rightarrow\:\mid{e}^{−{x}^{{n}} } \mathrm{cos}\lambda{x}\mid\leqslant{e}^{−{x}} \\ $$$$\mathrm{knowing}\:\mathrm{that}\:\int_{\mathrm{1}} ^{+\infty} {e}^{−{x}} {dx}=−{e}<\infty \\ $$$$\int_{\mathrm{0}} ^{+\infty} {e}^{−{x}^{{n}} } \mathrm{cos}\left(\lambda{x}\right){dx}\:\in\mathbb{R} \\ $$
Answered by TheHoneyCat last updated on 17/Jun/21
![let (a,b)∈(R_+ )^2 and l be this limit with ∫_0 ^(+∞) e^(−x^n ) cosλx dx =Re(∫_0 ^(+∞) e^(−(x^n +λix) ) dx) =Re([((−1)/λ)e^(−x^n ) e^(−λix) ]_0 ^(+∞) −∫_0 ^(+∞) ((nx^(n−1) )/λ)e^(−x^n ) e^(−iλx) dx) =Re(((−1)/λ)−∫_0 ^(+∞) ((nx^(n−1) )/λ)e^(−x^n ) e^(−iλx) dx) =((−1)/λ)−Re(∫_0 ^(+∞) ((nx^(n−1) )/λ)e^(−x^n ) e^(−iλx) dx) with λ sugiciently high =∣((nx^(n−1) )/λ)e^(−x^n ) e^(−iλx) ∣ =((nx^(n−1) )/λ)e^(−x^n ) ≤e^(−P(x)) with P some polynomial such that P(x)→_(x→+∞) +∞ e^(−P(x)) can be integrated, and is independent from λ thus: lim_(λ→+∞) ((−1)/λ)−Re(∫_0 ^(+∞) ((nx^(n−1) )/λ)e^(−x^n ) e^(−iλx) dx) =lim_(λ→+∞) ((−1)/λ)−Re(∫_0 ^(+∞) lim_(λ→+∞) ((nx^(n−1) )/λ)e^(−x^n ) e^(−iλx) dx) =0−Re(∫_0 ^(+∞) 0dx) =0_■](Q143719.png)
$$\mathrm{let}\:\left({a},{b}\right)\in\left(\mathbb{R}_{+} \right)^{\mathrm{2}} \:\mathrm{and}\:{l}\:\mathrm{be}\:\mathrm{this}\:\mathrm{limit} \\ $$$${with}\: \\ $$$$\int_{\mathrm{0}} ^{+\infty} {e}^{−{x}^{{n}} } \mathrm{cos}\lambda{x}\:{dx} \\ $$$$=\mathrm{Re}\left(\int_{\mathrm{0}} ^{+\infty} {e}^{−\left({x}^{{n}} \:+\lambda\boldsymbol{{i}}{x}\right)\:} {dx}\right) \\ $$$$=\mathrm{Re}\left(\left[\frac{−\mathrm{1}}{\lambda}{e}^{−{x}^{{n}} } {e}^{−\lambda\boldsymbol{{i}}{x}} \right]_{\mathrm{0}} ^{+\infty} −\int_{\mathrm{0}} ^{+\infty} \frac{{nx}^{{n}−\mathrm{1}} }{\lambda}{e}^{−{x}^{{n}} } {e}^{−\boldsymbol{{i}}\lambda{x}} {dx}\right) \\ $$$$=\mathrm{Re}\left(\frac{−\mathrm{1}}{\lambda}−\int_{\mathrm{0}} ^{+\infty} \frac{{nx}^{{n}−\mathrm{1}} }{\lambda}{e}^{−{x}^{{n}} } {e}^{−\boldsymbol{{i}}\lambda{x}} {dx}\right) \\ $$$$=\frac{−\mathrm{1}}{\lambda}−\mathrm{Re}\left(\int_{\mathrm{0}} ^{+\infty} \frac{{nx}^{{n}−\mathrm{1}} }{\lambda}{e}^{−{x}^{{n}} } {e}^{−\boldsymbol{{i}}\lambda{x}} {dx}\right) \\ $$$$\mathrm{with}\:\lambda\:{sugiciently}\:{high} \\ $$$$=\mid\frac{{nx}^{{n}−\mathrm{1}} }{\lambda}{e}^{−{x}^{{n}} } {e}^{−\boldsymbol{{i}}\lambda{x}} \mid \\ $$$$=\frac{{nx}^{{n}−\mathrm{1}} }{\lambda}{e}^{−{x}^{{n}} } \leqslant{e}^{−\mathrm{P}\left({x}\right)} \:\mathrm{with}\:\mathrm{P}\:\mathrm{some}\:\mathrm{polynomial}\:\mathrm{such}\:\mathrm{that}\:\mathrm{P}\left({x}\right)\underset{{x}\rightarrow+\infty} {\rightarrow}+\infty \\ $$$${e}^{−\mathrm{P}\left({x}\right)} \:\mathrm{can}\:\mathrm{be}\:\mathrm{integrated},\:\mathrm{and}\:\mathrm{is}\:\mathrm{independent}\:\mathrm{from}\:\lambda \\ $$$$\mathrm{thus}: \\ $$$${lim}_{\lambda\rightarrow+\infty} \frac{−\mathrm{1}}{\lambda}−\mathrm{Re}\left(\int_{\mathrm{0}} ^{+\infty} \frac{{nx}^{{n}−\mathrm{1}} }{\lambda}{e}^{−{x}^{{n}} } {e}^{−\boldsymbol{{i}}\lambda{x}} {dx}\right) \\ $$$$={lim}_{\lambda\rightarrow+\infty} \frac{−\mathrm{1}}{\lambda}−\mathrm{Re}\left(\int_{\mathrm{0}} ^{+\infty} {lim}_{\lambda\rightarrow+\infty} \frac{{nx}^{{n}−\mathrm{1}} }{\lambda}{e}^{−{x}^{{n}} } {e}^{−\boldsymbol{{i}}\lambda{x}} {dx}\right) \\ $$$$=\mathrm{0}−\mathrm{Re}\left(\int_{\mathrm{0}} ^{+\infty} \mathrm{0}{dx}\right) \\ $$$$=\mathrm{0}_{\blacksquare} \\ $$
Commented by mnjuly1970 last updated on 17/Jun/21

$${thanks}\:{alot}\:.... \\ $$
Commented by TheHoneyCat last updated on 17/Jun/21

$$\left.{your}\:{welcome}\::\bullet\right) \\ $$
