
Question Number 143109 by mnjuly1970 last updated on 10/Jun/21
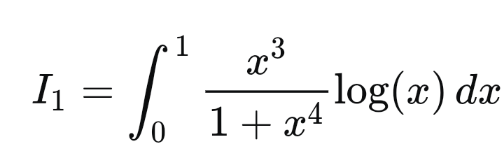
Commented by mnjuly1970 last updated on 10/Jun/21
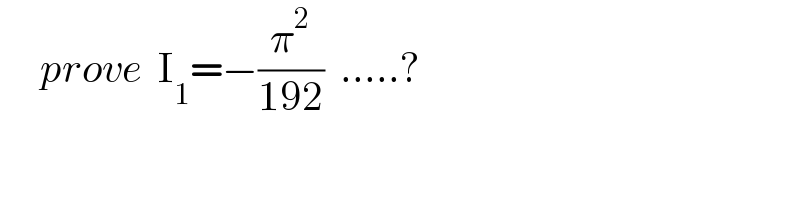
$$\:\:\:\:\:{prove}\:\:\mathrm{I}_{\mathrm{1}} =−\frac{\pi^{\mathrm{2}} }{\mathrm{192}}\:\:.....? \\ $$
Answered by qaz last updated on 10/Jun/21
![I_1 =∫_0 ^1 (x^3 /(1+x^4 ))lnxdx =(1/4)[ln(1+x^4 )lnx∣_0 ^1 −∫_0 ^1 ((ln(1+x^4 ))/x)dx] =−(1/4)Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^1 x^(4n−1) dx =−(1/4)Σ_(n=1) ^∞ (((−1)^(n−1) )/(4n^2 )) =−(1/(16))(1−2^(1−2) )ζ(2) =−(π^2 /(192))](Q143115.png)
$$\mathrm{I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{lnxdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)\mathrm{lnx}\mid_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}}\mathrm{dx}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{4n}−\mathrm{1}} \mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{4n}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−\mathrm{2}} \right)\zeta\left(\mathrm{2}\right) \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{192}} \\ $$
Commented by mnjuly1970 last updated on 10/Jun/21

$${thanks}\:{alot}... \\ $$
Answered by Ar Brandon last updated on 10/Jun/21
![I_1 =(1/4)[ln(1+x^4 )lnx−∫((ln(1+x^4 ))/x)dx]_0 ^1 =−(1/4)∫_0 ^1 Σ_(n=1) ^∞ (−1)^(n+1) (x^(4n−1) /n)=−Σ_(n=1) ^∞ (((−1)^(n+1) )/(16n^2 )) =−((η(2))/(16))=−((ζ(2))/(16))(1−(1/2))=−(π^2 /(192))](Q143118.png)
$$\mathrm{I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)\mathrm{lnx}−\int\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}}\mathrm{dx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \frac{\mathrm{x}^{\mathrm{4n}−\mathrm{1}} }{\mathrm{n}}=−\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{16n}^{\mathrm{2}} } \\ $$$$\:\:\:\:=−\frac{\eta\left(\mathrm{2}\right)}{\mathrm{16}}=−\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{16}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{192}} \\ $$
Commented by mnjuly1970 last updated on 10/Jun/21

$${grateful}.. \\ $$
Answered by Olaf_Thorendsen last updated on 10/Jun/21
![I_1 = ∫_0 ^1 (x^3 /(1+x^4 ))lnx dx I_1 = ∫_0 ^1 x^3 lnxΣ_(n=0) ^∞ (−1)^n x^(4n) dx I_1 = ∫_0 ^1 lnxΣ_(n=0) ^∞ (−1)^n x^(4n+3) dx I_1 = [lnxΣ_(n=0) ^∞ (−1)^n (x^(4n+4) /(4n+4))]_0 ^1 −∫_0 ^1 (1/x)Σ_(n=0) ^∞ (−1)^n (x^(4n+4) /(4n+4)) dx I_1 = −∫_0 ^1 Σ_(n=0) ^∞ (−1)^n (x^(4n+3) /(4n+4)) dx I_1 = −[Σ_(n=0) ^∞ (−1)^n (x^(4n+4) /((4n+4)^2 ))]_0 ^1 I_1 = −Σ_(n=0) ^∞ (((−1)^n )/((4n+4)^2 )) I_1 = (1/(16))Σ_(n=0) ^∞ (((−1)^(n+1) )/((n+1)^2 )) I_1 = (1/(16))Σ_(n=1) ^∞ (((−1)^n )/n^2 ) = (1/(16))(−(π^2 /(12))) = −(π^2 /(192))](Q143119.png)
$$\mathrm{I}_{\mathrm{1}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{4}} }\mathrm{ln}{x}\:{dx} \\ $$$$\mathrm{I}_{\mathrm{1}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{3}} \mathrm{ln}{x}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{4}{n}} \:{dx} \\ $$$$\mathrm{I}_{\mathrm{1}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}{x}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{4}{n}+\mathrm{3}} \:{dx} \\ $$$$\mathrm{I}_{\mathrm{1}} =\:\left[\mathrm{ln}{x}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{4}{n}+\mathrm{4}} }{\mathrm{4}{n}+\mathrm{4}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{4}{n}+\mathrm{4}} }{\mathrm{4}{n}+\mathrm{4}}\:{dx} \\ $$$$\mathrm{I}_{\mathrm{1}} \:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{4}{n}+\mathrm{3}} }{\mathrm{4}{n}+\mathrm{4}}\:{dx} \\ $$$$\mathrm{I}_{\mathrm{1}} \:=\:−\left[\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{4}{n}+\mathrm{4}} }{\left(\mathrm{4}{n}+\mathrm{4}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}_{\mathrm{1}} \:=\:−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{4}{n}+\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{16}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{16}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{16}}\left(−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\right)\:=\:−\frac{\pi^{\mathrm{2}} }{\mathrm{192}} \\ $$
Commented by mnjuly1970 last updated on 10/Jun/21

$$\:\:{mercey}\:{mr}\:{olaf}... \\ $$
