
Question Number 142717 by mohammad17 last updated on 04/Jun/21
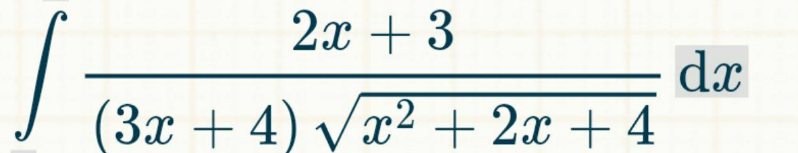
Commented by mohammad17 last updated on 04/Jun/21
$${it}\:{is}\:{very}\:{hard}\:{how}\:{can}\:{solve}\:{this} \\ $$
Answered by Ar Brandon last updated on 04/Jun/21
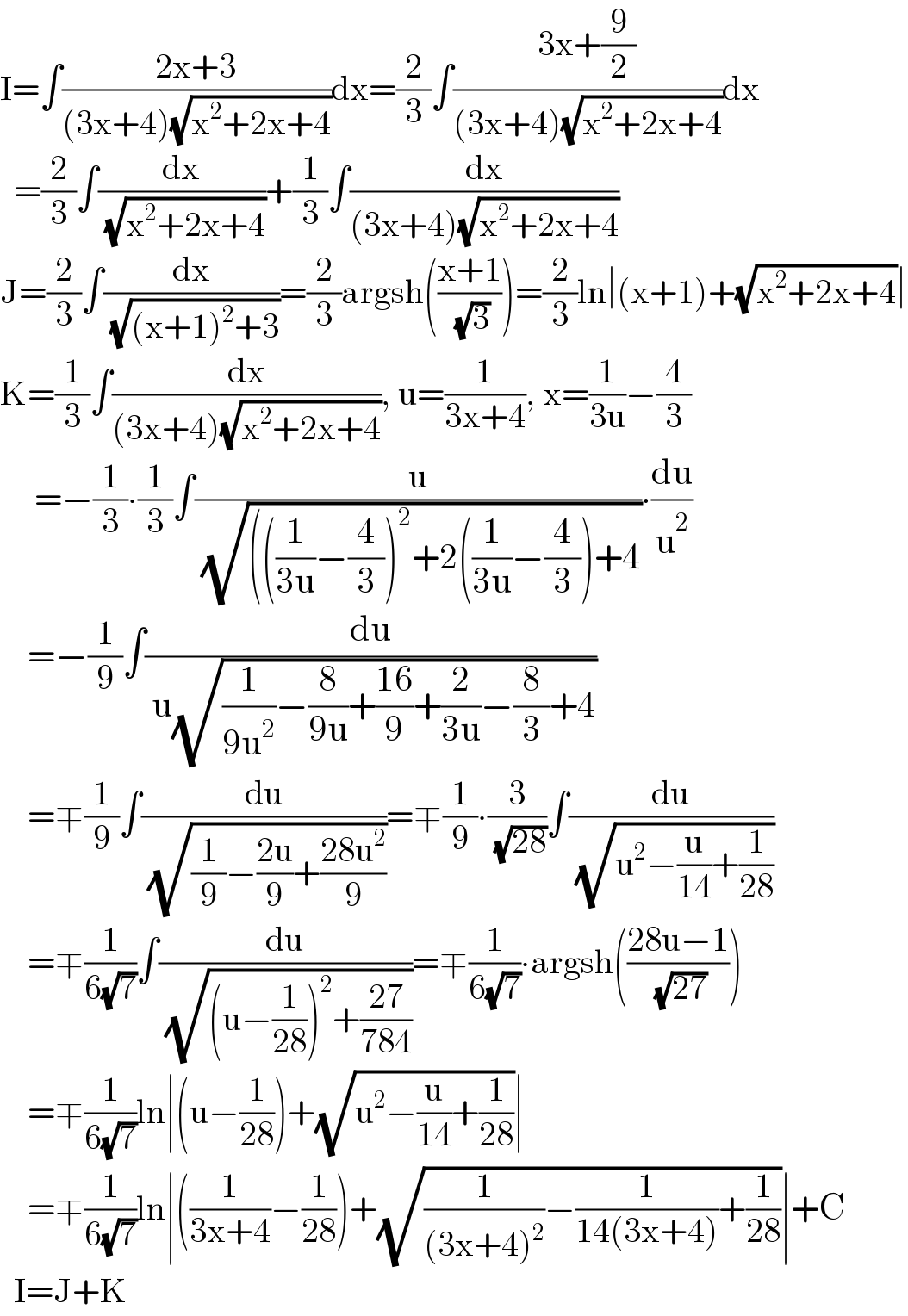
$$\mathrm{I}=\int\frac{\mathrm{2x}+\mathrm{3}}{\left(\mathrm{3x}+\mathrm{4}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{4}}}\mathrm{dx}=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{3x}+\frac{\mathrm{9}}{\mathrm{2}}}{\left(\mathrm{3x}+\mathrm{4}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{4}}}\mathrm{dx} \\ $$$$\:\:=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{4}}}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{dx}}{\left(\mathrm{3x}+\mathrm{4}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{4}}} \\ $$$$\mathrm{J}=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{dx}}{\:\sqrt{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}}}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{argsh}\left(\frac{\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\mid\left(\mathrm{x}+\mathrm{1}\right)+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{4}}\mid \\ $$$$\mathrm{K}=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{dx}}{\left(\mathrm{3x}+\mathrm{4}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{4}}},\:\mathrm{u}=\frac{\mathrm{1}}{\mathrm{3x}+\mathrm{4}},\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{3u}}−\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{u}}{\:\sqrt{\left(\left(\frac{\mathrm{1}}{\mathrm{3u}}−\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{3u}}−\frac{\mathrm{4}}{\mathrm{3}}\right)+\mathrm{4}\right.}}\centerdot\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} } \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{9}}\int\frac{\mathrm{du}}{\:\mathrm{u}\sqrt{\frac{\mathrm{1}}{\mathrm{9u}^{\mathrm{2}} }−\frac{\mathrm{8}}{\mathrm{9u}}+\frac{\mathrm{16}}{\mathrm{9}}+\frac{\mathrm{2}}{\mathrm{3u}}−\frac{\mathrm{8}}{\mathrm{3}}+\mathrm{4}}} \\ $$$$\:\:\:\:=\mp\frac{\mathrm{1}}{\mathrm{9}}\int\frac{\mathrm{du}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{2u}}{\mathrm{9}}+\frac{\mathrm{28u}^{\mathrm{2}} }{\mathrm{9}}}}=\mp\frac{\mathrm{1}}{\mathrm{9}}\centerdot\frac{\mathrm{3}}{\:\sqrt{\mathrm{28}}}\int\frac{\mathrm{du}}{\:\sqrt{\mathrm{u}^{\mathrm{2}} −\frac{\mathrm{u}}{\mathrm{14}}+\frac{\mathrm{1}}{\mathrm{28}}}} \\ $$$$\:\:\:\:=\mp\frac{\mathrm{1}}{\mathrm{6}\sqrt{\mathrm{7}}}\int\frac{\mathrm{du}}{\:\sqrt{\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{28}}\right)^{\mathrm{2}} +\frac{\mathrm{27}}{\mathrm{784}}}}=\mp\frac{\mathrm{1}}{\mathrm{6}\sqrt{\mathrm{7}}}\centerdot\mathrm{argsh}\left(\frac{\mathrm{28u}−\mathrm{1}}{\:\sqrt{\mathrm{27}}}\right) \\ $$$$\:\:\:\:=\mp\frac{\mathrm{1}}{\mathrm{6}\sqrt{\mathrm{7}}}\mathrm{ln}\mid\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{28}}\right)+\sqrt{\mathrm{u}^{\mathrm{2}} −\frac{\mathrm{u}}{\mathrm{14}}+\frac{\mathrm{1}}{\mathrm{28}}}\mid \\ $$$$\:\:\:\:=\mp\frac{\mathrm{1}}{\mathrm{6}\sqrt{\mathrm{7}}}\mathrm{ln}\mid\left(\frac{\mathrm{1}}{\mathrm{3x}+\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{28}}\right)+\sqrt{\frac{\mathrm{1}}{\left(\mathrm{3x}+\mathrm{4}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{14}\left(\mathrm{3x}+\mathrm{4}\right)}+\frac{\mathrm{1}}{\mathrm{28}}}\mid+\mathrm{C} \\ $$$$\:\:\mathrm{I}=\mathrm{J}+\mathrm{K} \\ $$
Answered by MJS_new last updated on 04/Jun/21
![((2x+3)/(3x+4))=(2/3)+(1/(3(3x+4))) ∫((2x+3)/((3x+4)(√(x^2 +2x+4))))dx= =(2/3)∫(dx/( (√(x^2 +2x+4))))+(1/3)∫(dx/((3x+4)(√(x^2 +2x+4))))= [t=x+1 → dx=dt] =(2/3)∫(dt/( (√(t^2 +3))))+(1/3)∫(dt/((3t+1)(√(t^2 +3))))= [u=((t+(√(t^2 +3)))/( (√3))) → dt=((√(3(t^2 +3)))/(t+(√(t^2 +3))))du=((√(t^2 +3))/u)du] (usually you would now substitute t=(√3)sinh u but I don′t like dealing with hyperbolic functions) =(2/3)∫(du/u)+((2(√3))/(27))∫(du/(u^2 +((2(√3))/9)u−1))= [v=u+((√3)/9) → du=dv] =(2/3)ln u +((2(√3))/(27))∫(dv/(v^2 −((28)/(27))))= [w=((3(√(21)))/(14))v → dv=((2(√(21)))/9)dw] =(2/3)ln u +((√7)/(21))∫(dw/(w^2 −1))= =(2/3)ln u +((√7)/(42))ln ((w−1)/(w+1)) = ... =(2/3)ln (x+1+(√(x^2 +2x+4))) +((√7)/(42))ln ∣((x−8+2(√(7(x^2 +2x+4))))/(3x+4))∣ +C](Q142731.png)
$$\frac{\mathrm{2}{x}+\mathrm{3}}{\mathrm{3}{x}+\mathrm{4}}=\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{3}{x}+\mathrm{4}\right)} \\ $$$$\int\frac{\mathrm{2}{x}+\mathrm{3}}{\left(\mathrm{3}{x}+\mathrm{4}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}}{dx}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\left(\mathrm{3}{x}+\mathrm{4}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\mathrm{1}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dt}}{\left(\mathrm{3}{t}+\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{{t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}{\:\sqrt{\mathrm{3}}}\:\rightarrow\:{dt}=\frac{\sqrt{\mathrm{3}\left({t}^{\mathrm{2}} +\mathrm{3}\right)}}{{t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}{du}=\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}{{u}}{du}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{usually}\:\mathrm{you}\:\mathrm{would}\:\mathrm{now}\:\mathrm{substitute}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{t}=\sqrt{\mathrm{3}}\mathrm{sinh}\:{u}\:\mathrm{but}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{like}\:\mathrm{dealing} \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{with}\:\mathrm{hyperbolic}\:\mathrm{functions}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{du}}{{u}}+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{27}}\int\frac{{du}}{{u}^{\mathrm{2}} +\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}{u}−\mathrm{1}}= \\ $$$$\:\:\:\:\:\left[{v}={u}+\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\:\rightarrow\:{du}={dv}\right] \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:{u}\:+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{27}}\int\frac{{dv}}{{v}^{\mathrm{2}} −\frac{\mathrm{28}}{\mathrm{27}}}= \\ $$$$\:\:\:\:\:\left[{w}=\frac{\mathrm{3}\sqrt{\mathrm{21}}}{\mathrm{14}}{v}\:\rightarrow\:{dv}=\frac{\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{9}}{dw}\right] \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:{u}\:+\frac{\sqrt{\mathrm{7}}}{\mathrm{21}}\int\frac{{dw}}{{w}^{\mathrm{2}} −\mathrm{1}}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:{u}\:+\frac{\sqrt{\mathrm{7}}}{\mathrm{42}}\mathrm{ln}\:\frac{{w}−\mathrm{1}}{{w}+\mathrm{1}}\:= \\ $$$$... \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:\left({x}+\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}\right)\:+\frac{\sqrt{\mathrm{7}}}{\mathrm{42}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{8}+\mathrm{2}\sqrt{\mathrm{7}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)}}{\mathrm{3}{x}+\mathrm{4}}\mid\:+{C} \\ $$
