
Question Number 142246 by mathdanisur last updated on 28/May/21
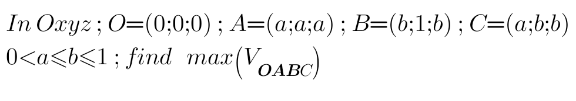
Answered by mr W last updated on 28/May/21
![V=(1/6) ((a,a,a),(b,1,b),(a,b,b) ) =(1/6)[a(b−b^2 )−a(b^2 −ab)+a(b^2 −a)] =(1/6)a(b−a)(1−b) ≤(1/6)×(((a+b−a+1−b)/3))^3 =(1/6)×(1/(27))=(1/(162)) ⇒V_(max) =(1/(162)) when a=b−a=1−b i.e. a=(1/3), b=(2/3)](Q142250.png)
$${V}=\frac{\mathrm{1}}{\mathrm{6}}\begin{pmatrix}{{a}}&{{a}}&{{a}}\\{{b}}&{\mathrm{1}}&{{b}}\\{{a}}&{{b}}&{{b}}\end{pmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[{a}\left({b}−{b}^{\mathrm{2}} \right)−{a}\left({b}^{\mathrm{2}} −{ab}\right)+{a}\left({b}^{\mathrm{2}} −{a}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}{a}\left({b}−{a}\right)\left(\mathrm{1}−{b}\right) \\ $$$$\leqslant\frac{\mathrm{1}}{\mathrm{6}}×\left(\frac{{a}+{b}−{a}+\mathrm{1}−{b}}{\mathrm{3}}\right)^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{6}}×\frac{\mathrm{1}}{\mathrm{27}}=\frac{\mathrm{1}}{\mathrm{162}} \\ $$$$\Rightarrow{V}_{{max}} =\frac{\mathrm{1}}{\mathrm{162}} \\ $$$${when}\:{a}={b}−{a}=\mathrm{1}−{b} \\ $$$${i}.{e}.\:{a}=\frac{\mathrm{1}}{\mathrm{3}},\:{b}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by mathdanisur last updated on 29/May/21
$${great}\:{Sir}\:{thank}\:{you} \\ $$
