
Question Number 141489 by mathsuji last updated on 19/May/21
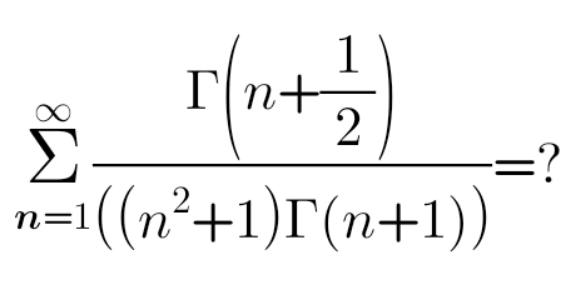
Answered by qaz last updated on 19/May/21
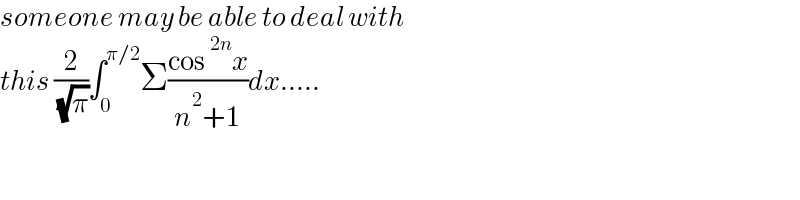
$${someone}\:{may}\:{be}\:{able}\:{to}\:{deal}\:{with}\: \\ $$$${this}\:\frac{\mathrm{2}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \Sigma\frac{\mathrm{cos}\:^{\mathrm{2}{n}} {x}}{{n}^{\mathrm{2}} +\mathrm{1}}{dx}..... \\ $$
Commented by mathsuji last updated on 19/May/21
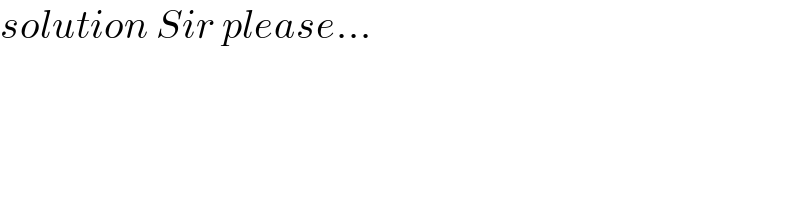
$${solution}\:{Sir}\:{please}... \\ $$
Answered by mindispower last updated on 19/May/21
![Γ(n+(1/2))=(n−(1/2)).....((1/2))Γ((1/2))=(√π).((1/2))_n n^2 +1=(n−i)(n+i) Γ(n+1)=n! Σ_(n≥1) ((((1/2))_n .(√π))/((n+i)(n−i))) (n+i)=(((i)_n )/((1+i)_n )) ⇔Σ_(n≥1) (((√π).((1/2))_n .(1+i)_n (1−i)_n )/((i)_n (−i)_n )).(1/(n!)) =(√π) ( _3 F_2 ((1/2),(1+i),1−i;i,−i;[1])−1) Wher _3 F_2 is generealized Hyper geometric Function](Q141503.png)
$$\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right).....\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi}.\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} \\ $$$${n}^{\mathrm{2}} +\mathrm{1}=\left({n}−{i}\right)\left({n}+{i}\right) \\ $$$$\Gamma\left({n}+\mathrm{1}\right)={n}! \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} .\sqrt{\pi}}{\left({n}+{i}\right)\left({n}−{i}\right)} \\ $$$$\left({n}+{i}\right)=\frac{\left({i}\right)_{{n}} }{\left(\mathrm{1}+{i}\right)_{{n}} } \\ $$$$\Leftrightarrow\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\sqrt{\pi}.\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} .\left(\mathrm{1}+{i}\right)_{{n}} \left(\mathrm{1}−{i}\right)_{{n}} }{\left({i}\right)_{{n}} \left(−{i}\right)_{{n}} }.\frac{\mathrm{1}}{{n}!} \\ $$$$=\sqrt{\pi}\:\:\left(\:\:_{\mathrm{3}} {F}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}},\left(\mathrm{1}+{i}\right),\mathrm{1}−{i};{i},−{i};\left[\mathrm{1}\right]\right)−\mathrm{1}\right) \\ $$$${Wher}\:_{\mathrm{3}} {F}_{\mathrm{2}} \:{is}\:{generealized}\:{Hyper}\:{geometric}\:{Function} \\ $$$$ \\ $$
