
Question Number 141017 by 777316 last updated on 14/May/21

Commented by mnjuly1970 last updated on 15/May/21

$$\:\:{hello}\:{mr}\:: \\ $$$$\:\:{what}\:``{font}``\:{and}\:``\:{app}``\:{did}\:{you} \\ $$$$\:{use}\:{to}\:{write}\:{math}?? \\ $$$$\:\: \\ $$
Answered by mnjuly1970 last updated on 14/May/21
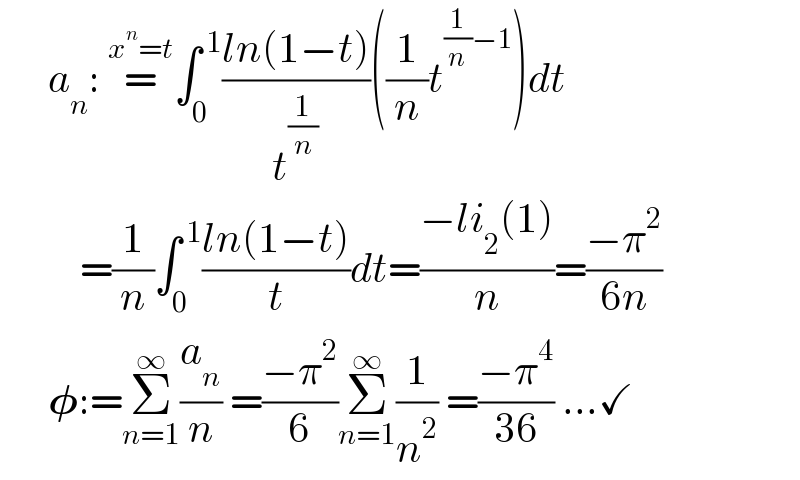
$$\:\:\:\:\:\:{a}_{{n}} :\:\overset{{x}^{{n}} ={t}} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}^{\frac{\mathrm{1}}{{n}}} }\left(\frac{\mathrm{1}}{{n}}{t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \right){dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt}=\frac{−{li}_{\mathrm{2}} \left(\mathrm{1}\right)}{{n}}=\frac{−\pi^{\mathrm{2}} }{\mathrm{6}{n}} \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{a}_{{n}} }{{n}}\:=\frac{−\pi^{\mathrm{2}} }{\mathrm{6}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{−\pi^{\mathrm{4}} }{\mathrm{36}}\:...\checkmark \\ $$
Answered by Dwaipayan Shikari last updated on 14/May/21
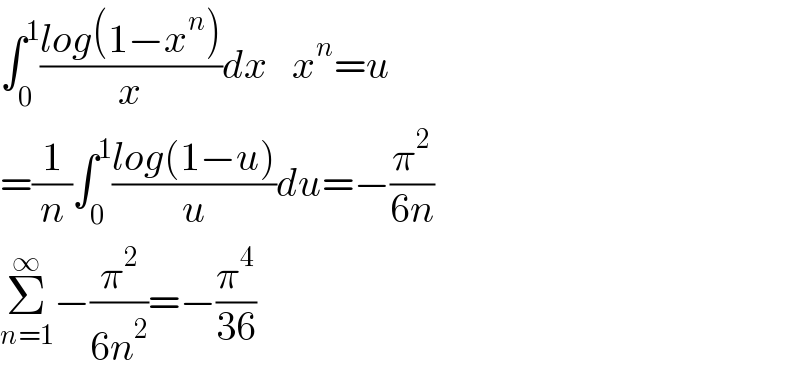
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}−{x}^{{n}} \right)}{{x}}{dx}\:\:\:{x}^{{n}} ={u} \\ $$$$=\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}−{u}\right)}{{u}}{du}=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}{n}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}−\frac{\pi^{\mathrm{2}} }{\mathrm{6}{n}^{\mathrm{2}} }=−\frac{\pi^{\mathrm{4}} }{\mathrm{36}} \\ $$
