Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 140550 by liberty last updated on 09/May/21

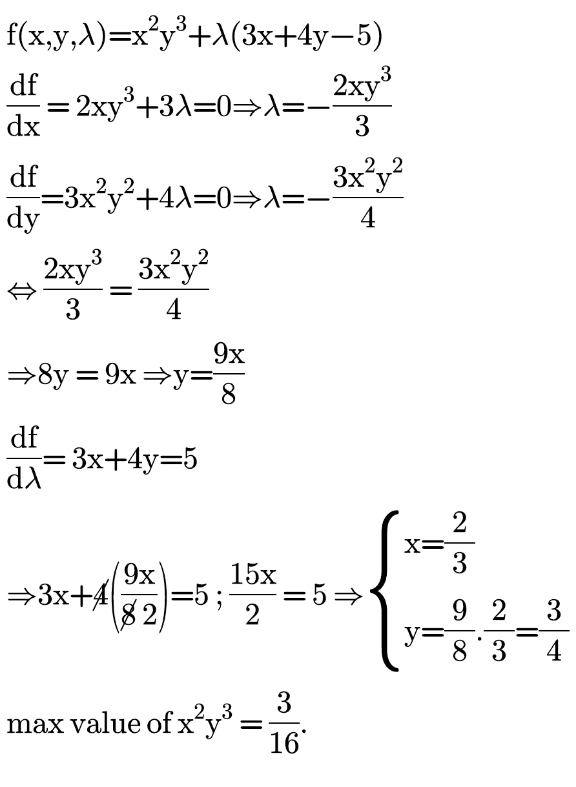
Commented by mr W last updated on 09/May/21

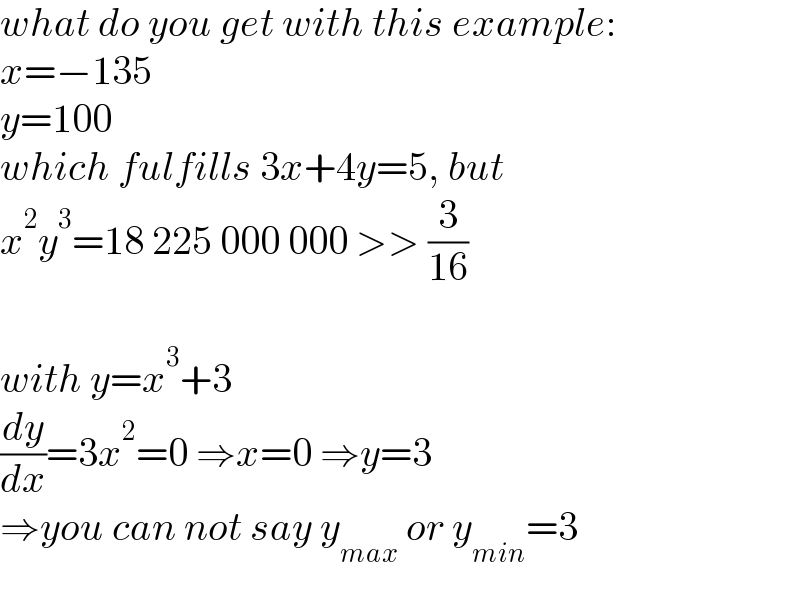
what do you get with this example: x=−135 y=100 which fulfills 3x+4y=5, but x^2 y^3 =18 225 000 000 >> (3/(16)) with y=x^3 +3 (dy/dx)=3x^2 =0 ⇒x=0 ⇒y=3 ⇒you can not say y_(max) or y_(min) =3

$${what}\:{do}\:{you}\:{get}\:{with}\:{this}\:{example}: \\ $$$${x}=−\mathrm{135} \\ $$$${y}=\mathrm{100} \\ $$$${which}\:{fulfills}\:\mathrm{3}{x}+\mathrm{4}{y}=\mathrm{5},\:{but} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{3}} =\mathrm{18}\:\mathrm{225}\:\mathrm{000}\:\mathrm{000}\:>>\:\frac{\mathrm{3}}{\mathrm{16}} \\ $$$$ \\ $$$${with}\:{y}={x}^{\mathrm{3}} +\mathrm{3} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{3}{x}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow{x}=\mathrm{0}\:\Rightarrow{y}=\mathrm{3} \\ $$$$\Rightarrow{you}\:{can}\:{not}\:{say}\:{y}_{{max}} \:{or}\:{y}_{{min}} =\mathrm{3} \\ $$

Commented by liberty last updated on 09/May/21

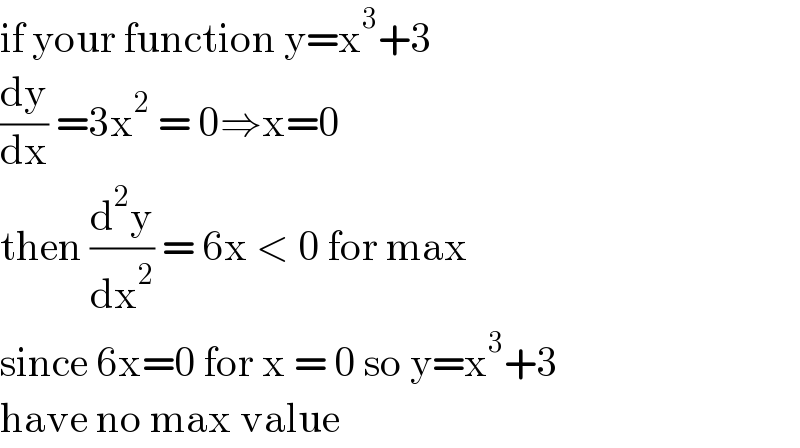
if your function y=x^3 +3 (dy/dx) =3x^2 = 0⇒x=0 then (d^2 y/dx^2 ) = 6x < 0 for max since 6x=0 for x = 0 so y=x^3 +3 have no max value

$$\mathrm{if}\:\mathrm{your}\:\mathrm{function}\:\mathrm{y}=\mathrm{x}^{\mathrm{3}} +\mathrm{3} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\mathrm{3x}^{\mathrm{2}} \:=\:\mathrm{0}\Rightarrow\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{then}\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:\mathrm{6x}\:<\:\mathrm{0}\:\mathrm{for}\:\mathrm{max} \\ $$$$\mathrm{since}\:\mathrm{6x}=\mathrm{0}\:\mathrm{for}\:\mathrm{x}\:=\:\mathrm{0}\:\mathrm{so}\:\mathrm{y}=\mathrm{x}^{\mathrm{3}} +\mathrm{3} \\ $$$$\mathrm{have}\:\mathrm{no}\:\mathrm{max}\:\mathrm{value} \\ $$

Commented by liberty last updated on 09/May/21

3x+4y=5⇒x=((5−4y)/3) f(y)=(((5−4y)/3))^2 y^3 f ′(y)=−(8/3)y^3 (((5−4y)/3))+3y^2 (((5−4y)/3))^2 =0 y^2 (((5−4y)/3))[−(8/3)y+3(((5−4y)/3))]=0 y^2 (((5−4y)/3))[((−20y+15)/3)]=0 y=0; (5/4) ; (3/4) ⇒f(y) decreasing for (3/4)<y<(5/4) and increasing for y<0 ∪ 0<y<(3/4) ∪ y>(5/4) so y=(3/4) is critical point

$$\mathrm{3x}+\mathrm{4y}=\mathrm{5}\Rightarrow\mathrm{x}=\frac{\mathrm{5}−\mathrm{4y}}{\mathrm{3}} \\ $$$$\mathrm{f}\left(\mathrm{y}\right)=\left(\frac{\mathrm{5}−\mathrm{4y}}{\mathrm{3}}\right)^{\mathrm{2}} \mathrm{y}^{\mathrm{3}} \\ $$$$\mathrm{f}\:'\left(\mathrm{y}\right)=−\frac{\mathrm{8}}{\mathrm{3}}\mathrm{y}^{\mathrm{3}} \left(\frac{\mathrm{5}−\mathrm{4y}}{\mathrm{3}}\right)+\mathrm{3y}^{\mathrm{2}} \left(\frac{\mathrm{5}−\mathrm{4y}}{\mathrm{3}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{y}^{\mathrm{2}} \left(\frac{\mathrm{5}−\mathrm{4y}}{\mathrm{3}}\right)\left[−\frac{\mathrm{8}}{\mathrm{3}}\mathrm{y}+\mathrm{3}\left(\frac{\mathrm{5}−\mathrm{4y}}{\mathrm{3}}\right)\right]=\mathrm{0} \\ $$$$\mathrm{y}^{\mathrm{2}} \left(\frac{\mathrm{5}−\mathrm{4y}}{\mathrm{3}}\right)\left[\frac{−\mathrm{20y}+\mathrm{15}}{\mathrm{3}}\right]=\mathrm{0} \\ $$$$\mathrm{y}=\mathrm{0};\:\frac{\mathrm{5}}{\mathrm{4}}\:;\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{y}\right)\:\mathrm{decreasing}\:\mathrm{for}\:\frac{\mathrm{3}}{\mathrm{4}}<\mathrm{y}<\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\mathrm{and}\:\mathrm{increasing}\:\mathrm{for}\:\mathrm{y}<\mathrm{0}\:\cup\:\mathrm{0}<\mathrm{y}<\frac{\mathrm{3}}{\mathrm{4}}\:\cup\:\mathrm{y}>\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\mathrm{so}\:\mathrm{y}=\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{is}\:\mathrm{critical}\:\mathrm{point} \\ $$

Commented by mr W last updated on 09/May/21

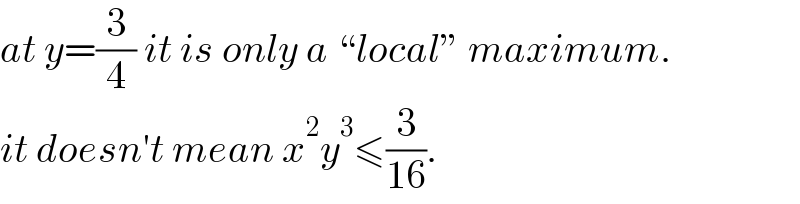
at y=(3/4) it is only a “local” maximum. it doesn′t mean x^2 y^3 ≤(3/(16)).

$${at}\:{y}=\frac{\mathrm{3}}{\mathrm{4}}\:{it}\:{is}\:{only}\:{a}\:``{local}''\:{maximum}. \\ $$$${it}\:{doesn}'{t}\:{mean}\:{x}^{\mathrm{2}} {y}^{\mathrm{3}} \leqslant\frac{\mathrm{3}}{\mathrm{16}}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com