Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 140367 by aliibrahim1 last updated on 06/May/21

Answered by meetbhavsar25 last updated on 06/May/21

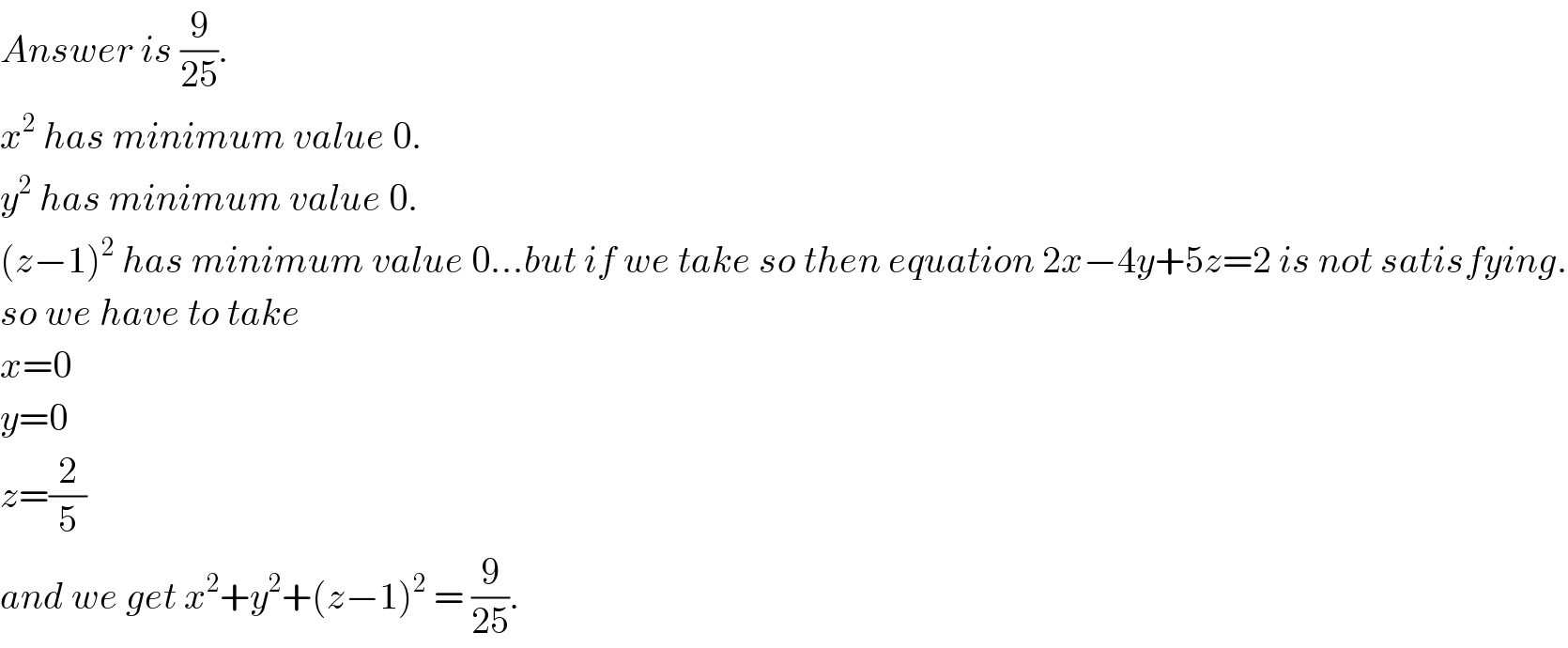
Answer is (9/(25)). x^2 has minimum value 0. y^2 has minimum value 0. (z−1)^2 has minimum value 0...but if we take so then equation 2x−4y+5z=2 is not satisfying. so we have to take x=0 y=0 z=(2/5) and we get x^2 +y^2 +(z−1)^2 = (9/(25)).

$${Answer}\:{is}\:\frac{\mathrm{9}}{\mathrm{25}}. \\ $$$${x}^{\mathrm{2}} \:{has}\:{minimum}\:{value}\:\mathrm{0}. \\ $$$${y}^{\mathrm{2}} \:{has}\:{minimum}\:{value}\:\mathrm{0}. \\ $$$$\left({z}−\mathrm{1}\right)^{\mathrm{2}} \:{has}\:{minimum}\:{value}\:\mathrm{0}...{but}\:{if}\:{we}\:{take}\:{so}\:{then}\:{equation}\:\mathrm{2}{x}−\mathrm{4}{y}+\mathrm{5}{z}=\mathrm{2}\:{is}\:{not}\:{satisfying}. \\ $$$${so}\:{we}\:{have}\:{to}\:{take}\: \\ $$$${x}=\mathrm{0} \\ $$$${y}=\mathrm{0} \\ $$$${z}=\frac{\mathrm{2}}{\mathrm{5}} \\ $$$${and}\:{we}\:{get}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({z}−\mathrm{1}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{9}}{\mathrm{25}}. \\ $$

Commented by aliibrahim1 last updated on 06/May/21

thx dir appreciate it

$${thx}\:{dir}\:{appreciate}\:{it} \\ $$

Commented by aliibrahim1 last updated on 06/May/21

your answer is incorrect sir

$${your}\:{answer}\:{is}\:{incorrect}\:{sir} \\ $$

Commented by meetbhavsar25 last updated on 07/May/21

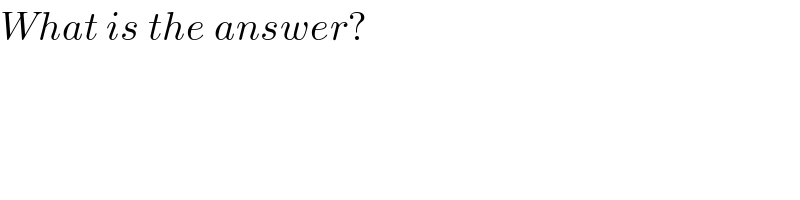
What is the answer?

$${What}\:{is}\:{the}\:{answer}? \\ $$

Commented by meetbhavsar25 last updated on 07/May/21

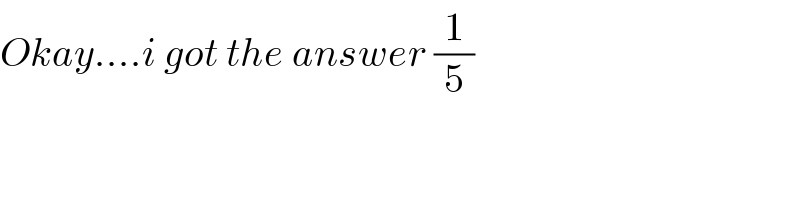
Okay....i got the answer (1/5)

$${Okay}....{i}\:{got}\:{the}\:{answer}\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$

Commented by aliibrahim1 last updated on 07/May/21

yes correct

$${yes}\:{correct} \\ $$

Answered by mr W last updated on 06/May/21

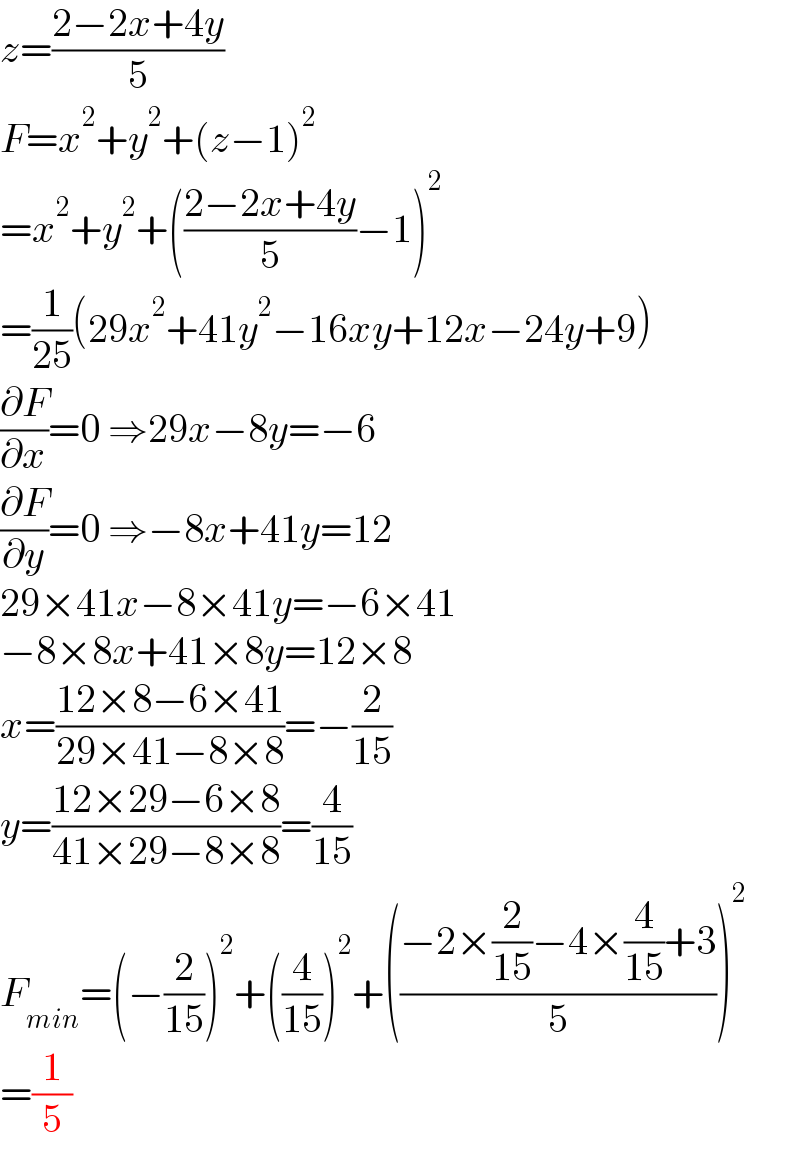
z=((2−2x+4y)/5) F=x^2 +y^2 +(z−1)^2 =x^2 +y^2 +(((2−2x+4y)/5)−1)^2 =(1/(25))(29x^2 +41y^2 −16xy+12x−24y+9) (∂F/∂x)=0 ⇒29x−8y=−6 (∂F/∂y)=0 ⇒−8x+41y=12 29×41x−8×41y=−6×41 −8×8x+41×8y=12×8 x=((12×8−6×41)/(29×41−8×8))=−(2/(15)) y=((12×29−6×8)/(41×29−8×8))=(4/(15)) F_(min) =(−(2/(15)))^2 +((4/(15)))^2 +(((−2×(2/(15))−4×(4/(15))+3)/5))^2 =(1/5)

$${z}=\frac{\mathrm{2}−\mathrm{2}{x}+\mathrm{4}{y}}{\mathrm{5}} \\ $$$${F}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({z}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left(\frac{\mathrm{2}−\mathrm{2}{x}+\mathrm{4}{y}}{\mathrm{5}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{25}}\left(\mathrm{29}{x}^{\mathrm{2}} +\mathrm{41}{y}^{\mathrm{2}} −\mathrm{16}{xy}+\mathrm{12}{x}−\mathrm{24}{y}+\mathrm{9}\right) \\ $$$$\frac{\partial{F}}{\partial{x}}=\mathrm{0}\:\Rightarrow\mathrm{29}{x}−\mathrm{8}{y}=−\mathrm{6} \\ $$$$\frac{\partial{F}}{\partial{y}}=\mathrm{0}\:\Rightarrow−\mathrm{8}{x}+\mathrm{41}{y}=\mathrm{12} \\ $$$$\mathrm{29}×\mathrm{41}{x}−\mathrm{8}×\mathrm{41}{y}=−\mathrm{6}×\mathrm{41} \\ $$$$−\mathrm{8}×\mathrm{8}{x}+\mathrm{41}×\mathrm{8}{y}=\mathrm{12}×\mathrm{8} \\ $$$${x}=\frac{\mathrm{12}×\mathrm{8}−\mathrm{6}×\mathrm{41}}{\mathrm{29}×\mathrm{41}−\mathrm{8}×\mathrm{8}}=−\frac{\mathrm{2}}{\mathrm{15}} \\ $$$${y}=\frac{\mathrm{12}×\mathrm{29}−\mathrm{6}×\mathrm{8}}{\mathrm{41}×\mathrm{29}−\mathrm{8}×\mathrm{8}}=\frac{\mathrm{4}}{\mathrm{15}} \\ $$$${F}_{{min}} =\left(−\frac{\mathrm{2}}{\mathrm{15}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{15}}\right)^{\mathrm{2}} +\left(\frac{−\mathrm{2}×\frac{\mathrm{2}}{\mathrm{15}}−\mathrm{4}×\frac{\mathrm{4}}{\mathrm{15}}+\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}} \\ $$

Commented by mr W last updated on 06/May/21

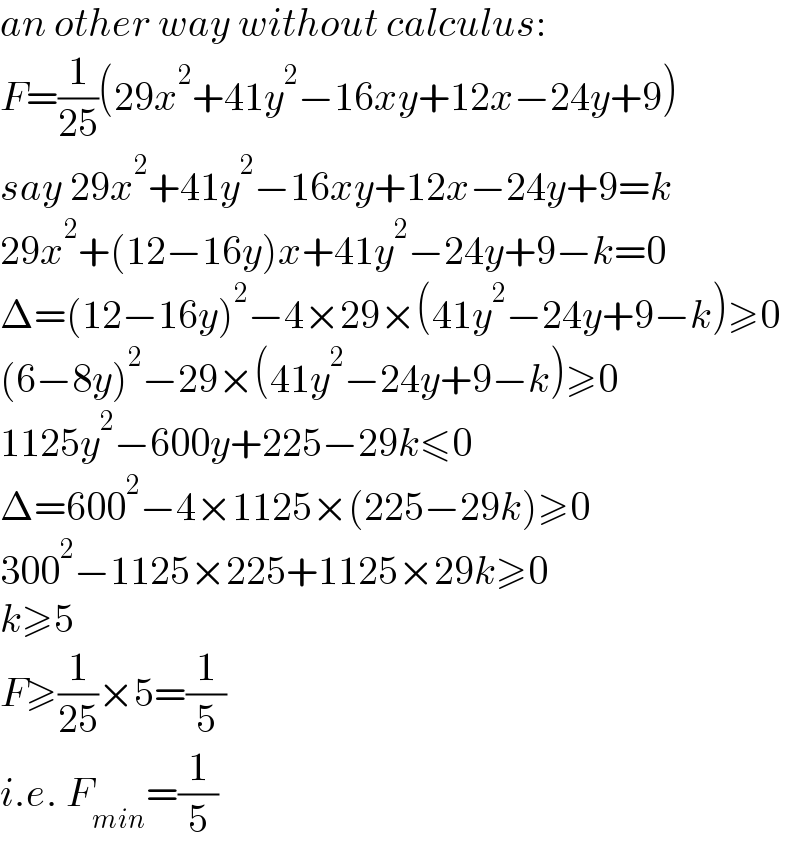
an other way without calculus: F=(1/(25))(29x^2 +41y^2 −16xy+12x−24y+9) say 29x^2 +41y^2 −16xy+12x−24y+9=k 29x^2 +(12−16y)x+41y^2 −24y+9−k=0 Δ=(12−16y)^2 −4×29×(41y^2 −24y+9−k)≥0 (6−8y)^2 −29×(41y^2 −24y+9−k)≥0 1125y^2 −600y+225−29k≤0 Δ=600^2 −4×1125×(225−29k)≥0 300^2 −1125×225+1125×29k≥0 k≥5 F≥(1/(25))×5=(1/5) i.e. F_(min) =(1/5)

$${an}\:{other}\:{way}\:{without}\:{calculus}: \\ $$$${F}=\frac{\mathrm{1}}{\mathrm{25}}\left(\mathrm{29}{x}^{\mathrm{2}} +\mathrm{41}{y}^{\mathrm{2}} −\mathrm{16}{xy}+\mathrm{12}{x}−\mathrm{24}{y}+\mathrm{9}\right) \\ $$$${say}\:\mathrm{29}{x}^{\mathrm{2}} +\mathrm{41}{y}^{\mathrm{2}} −\mathrm{16}{xy}+\mathrm{12}{x}−\mathrm{24}{y}+\mathrm{9}={k} \\ $$$$\mathrm{29}{x}^{\mathrm{2}} +\left(\mathrm{12}−\mathrm{16}{y}\right){x}+\mathrm{41}{y}^{\mathrm{2}} −\mathrm{24}{y}+\mathrm{9}−{k}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{12}−\mathrm{16}{y}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{29}×\left(\mathrm{41}{y}^{\mathrm{2}} −\mathrm{24}{y}+\mathrm{9}−{k}\right)\geqslant\mathrm{0} \\ $$$$\left(\mathrm{6}−\mathrm{8}{y}\right)^{\mathrm{2}} −\mathrm{29}×\left(\mathrm{41}{y}^{\mathrm{2}} −\mathrm{24}{y}+\mathrm{9}−{k}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{1125}{y}^{\mathrm{2}} −\mathrm{600}{y}+\mathrm{225}−\mathrm{29}{k}\leqslant\mathrm{0} \\ $$$$\Delta=\mathrm{600}^{\mathrm{2}} −\mathrm{4}×\mathrm{1125}×\left(\mathrm{225}−\mathrm{29}{k}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{300}^{\mathrm{2}} −\mathrm{1125}×\mathrm{225}+\mathrm{1125}×\mathrm{29}{k}\geqslant\mathrm{0} \\ $$$${k}\geqslant\mathrm{5} \\ $$$${F}\geqslant\frac{\mathrm{1}}{\mathrm{25}}×\mathrm{5}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${i}.{e}.\:{F}_{{min}} =\frac{\mathrm{1}}{\mathrm{5}} \\ $$

Commented by aliibrahim1 last updated on 07/May/21

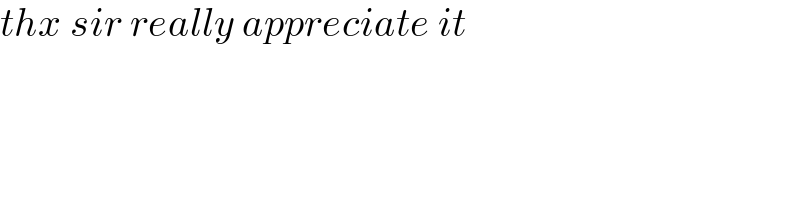
thx sir really appreciate it

$${thx}\:{sir}\:{really}\:{appreciate}\:{it} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com