
Question Number 140139 by mathsuji last updated on 04/May/21
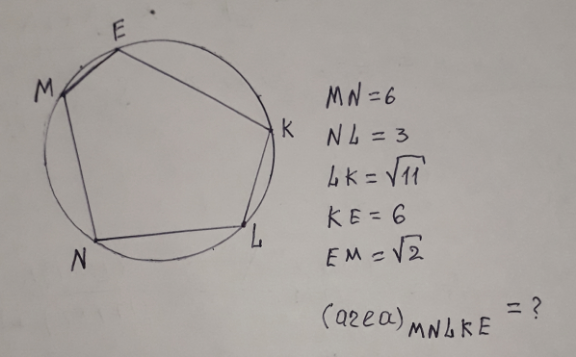
Answered by mr W last updated on 04/May/21
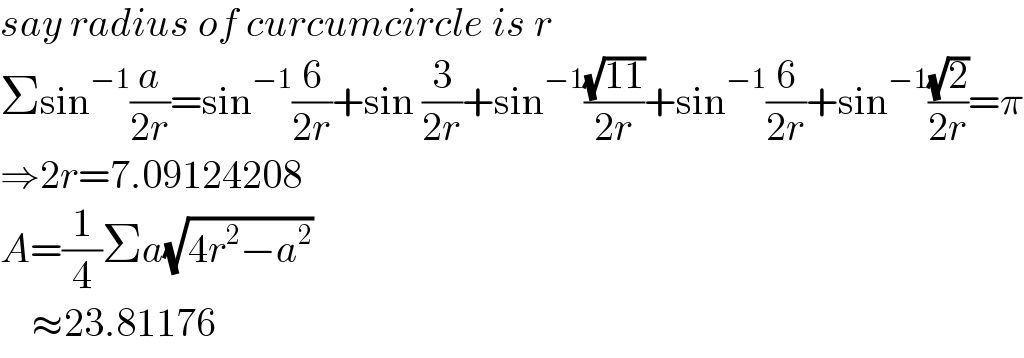
$${say}\:{radius}\:{of}\:{curcumcircle}\:{is}\:{r} \\ $$$$\Sigma\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{r}}=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{6}}{\mathrm{2}{r}}+\mathrm{sin}\:\frac{\mathrm{3}}{\mathrm{2}{r}}+\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{11}}}{\mathrm{2}{r}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{6}}{\mathrm{2}{r}}+\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}}{\mathrm{2}{r}}=\pi \\ $$$$\Rightarrow\mathrm{2}{r}=\mathrm{7}.\mathrm{09124208} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{4}}\Sigma{a}\sqrt{\mathrm{4}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$\:\:\:\:\approx\mathrm{23}.\mathrm{81176} \\ $$
Commented by mr W last updated on 04/May/21
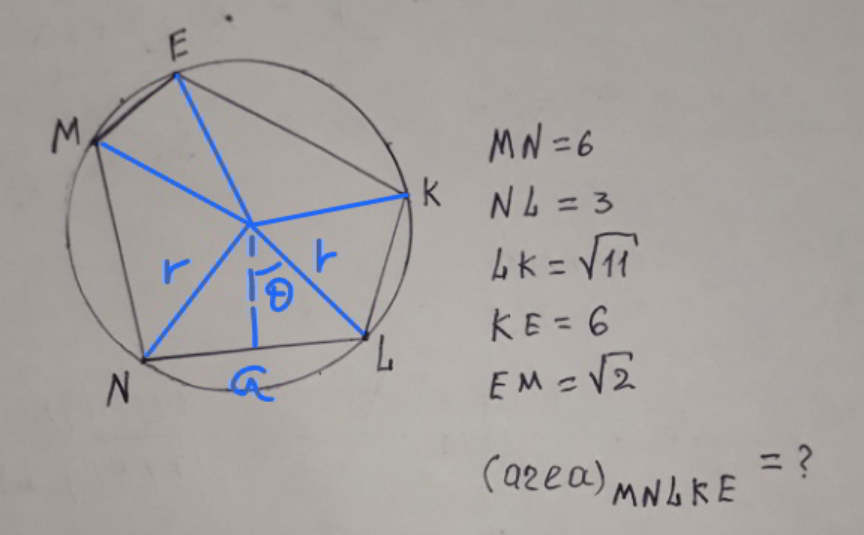
Commented by mathsuji last updated on 05/May/21
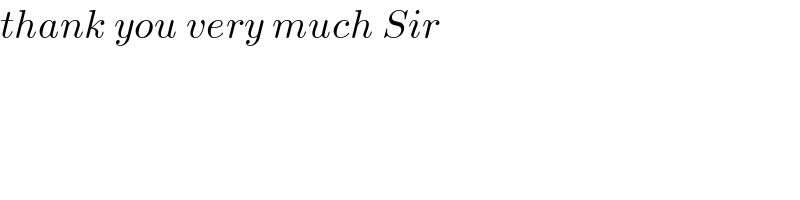
$${thank}\:{you}\:{very}\:{much}\:{Sir} \\ $$
