
Question Number 140053 by ajfour last updated on 03/May/21
Commented by ajfour last updated on 03/May/21

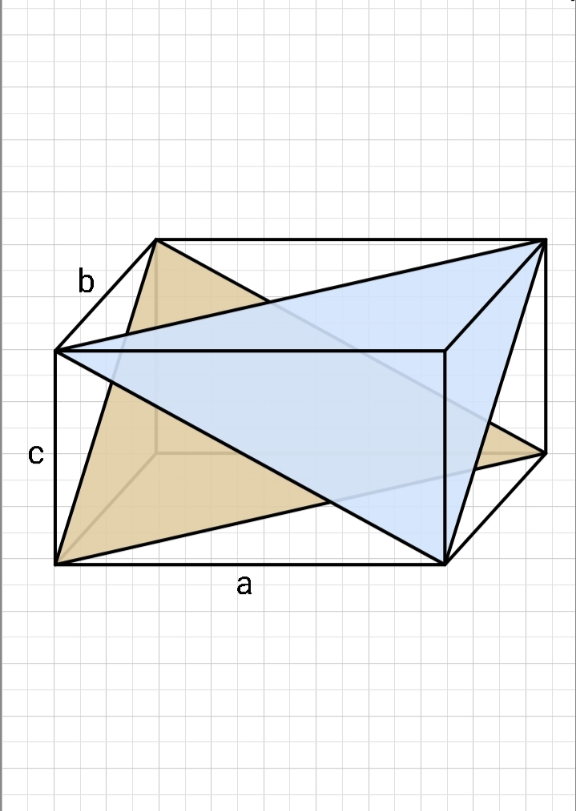
$${Find}\:{radius}\:{of}\:{largest}\:{sphere}\: \\ $$$${within}\:{the}\:{cuboid}\:{and}\:{between} \\ $$$${the}\:{shown}\:{triangular}\:{planes}. \\ $$
Commented by MJS_new last updated on 03/May/21
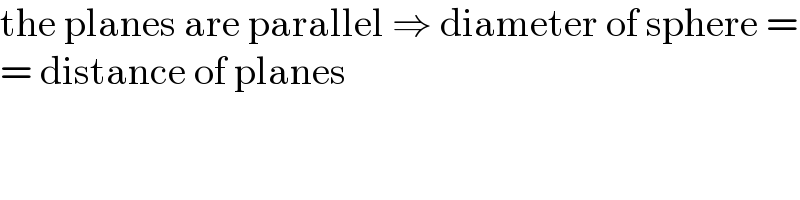
$$\mathrm{the}\:\mathrm{planes}\:\mathrm{are}\:\mathrm{parallel}\:\Rightarrow\:\mathrm{diameter}\:\mathrm{of}\:\mathrm{sphere}\:= \\ $$$$=\:\mathrm{distance}\:\mathrm{of}\:\mathrm{planes} \\ $$
Commented by mr W last updated on 03/May/21
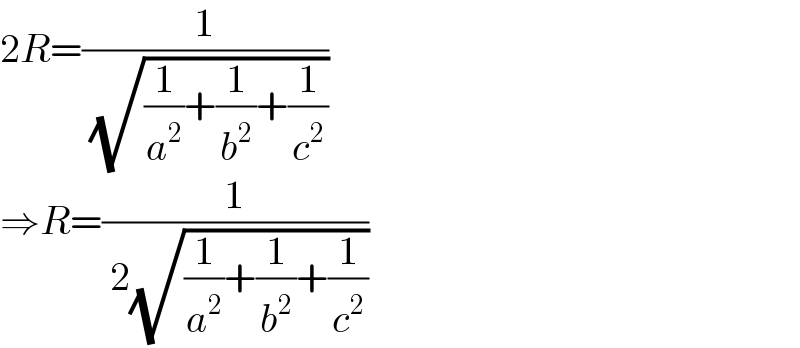
$$\mathrm{2}{R}=\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }}} \\ $$$$\Rightarrow{R}=\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }}} \\ $$
