
Question Number 139171 by mnjuly1970 last updated on 23/Apr/21

Answered by Dwaipayan Shikari last updated on 23/Apr/21
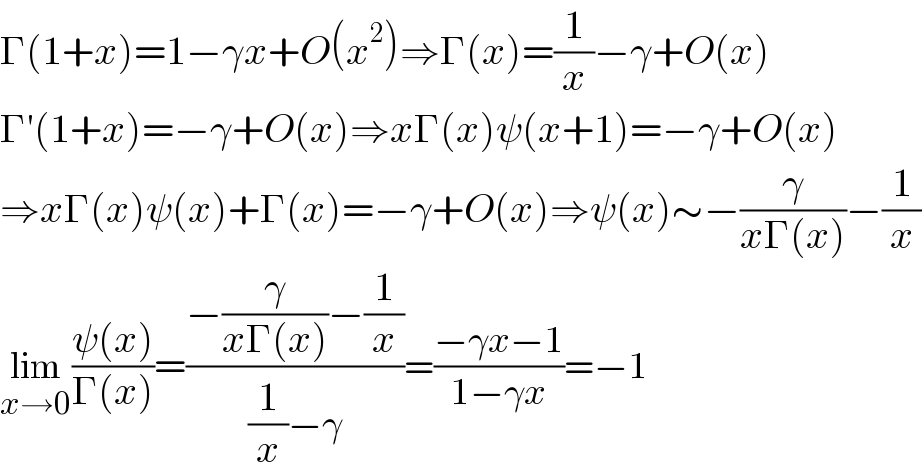
$$\Gamma\left(\mathrm{1}+{x}\right)=\mathrm{1}−\gamma{x}+{O}\left({x}^{\mathrm{2}} \right)\Rightarrow\Gamma\left({x}\right)=\frac{\mathrm{1}}{{x}}−\gamma+{O}\left({x}\right) \\ $$$$\Gamma'\left(\mathrm{1}+{x}\right)=−\gamma+{O}\left({x}\right)\Rightarrow{x}\Gamma\left({x}\right)\psi\left({x}+\mathrm{1}\right)=−\gamma+{O}\left({x}\right) \\ $$$$\Rightarrow{x}\Gamma\left({x}\right)\psi\left({x}\right)+\Gamma\left({x}\right)=−\gamma+{O}\left({x}\right)\Rightarrow\psi\left({x}\right)\sim−\frac{\gamma}{{x}\Gamma\left({x}\right)}−\frac{\mathrm{1}}{{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\psi\left({x}\right)}{\Gamma\left({x}\right)}=\frac{−\frac{\gamma}{{x}\Gamma\left({x}\right)}−\frac{\mathrm{1}}{{x}}}{\frac{\mathrm{1}}{{x}}−\gamma}=\frac{−\gamma{x}−\mathrm{1}}{\mathrm{1}−\gamma{x}}=−\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 24/Apr/21

$${mercey} \\ $$
Answered by Kamel last updated on 24/Apr/21
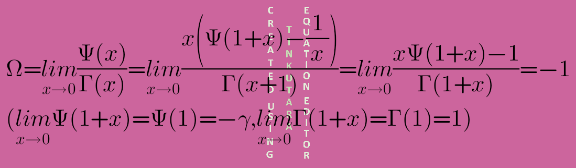
Commented by mnjuly1970 last updated on 24/Apr/21

$${mercey}\:... \\ $$
