
Question Number 138702 by peter frank last updated on 16/Apr/21
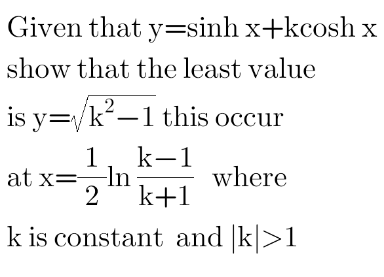
Answered by mr W last updated on 17/Apr/21
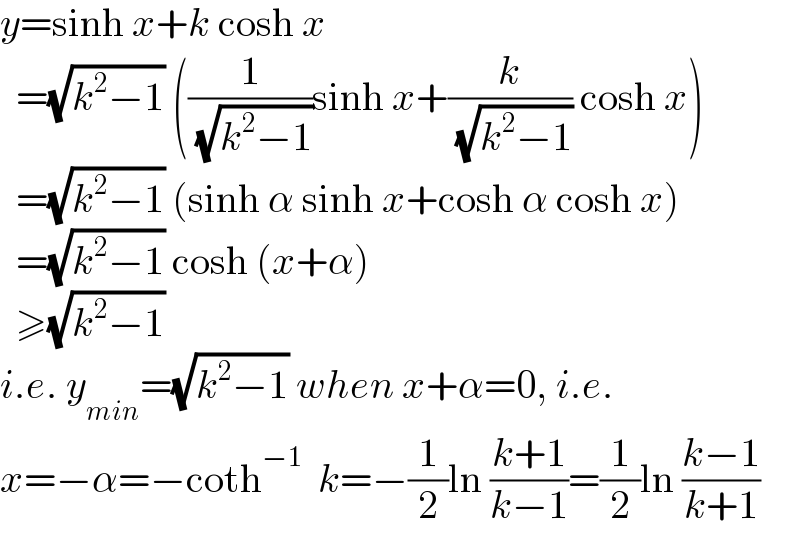
$${y}=\mathrm{sinh}\:{x}+{k}\:\mathrm{cosh}\:{x} \\ $$$$\:\:=\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}\:\left(\frac{\mathrm{1}}{\:\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}}\mathrm{sinh}\:{x}+\frac{{k}}{\:\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}}\:\mathrm{cosh}\:{x}\right) \\ $$$$\:\:=\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}\:\left(\mathrm{sinh}\:\alpha\:\mathrm{sinh}\:{x}+\mathrm{cosh}\:\alpha\:\mathrm{cosh}\:{x}\right) \\ $$$$\:\:=\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{cosh}\:\left({x}+\alpha\right) \\ $$$$\:\:\geqslant\sqrt{{k}^{\mathrm{2}} −\mathrm{1}} \\ $$$${i}.{e}.\:{y}_{{min}} =\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}\:{when}\:{x}+\alpha=\mathrm{0},\:{i}.{e}. \\ $$$${x}=−\alpha=−\mathrm{coth}^{−\mathrm{1}} \:\:{k}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{k}+\mathrm{1}}{{k}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}} \\ $$
Commented by peter frank last updated on 17/Apr/21
$${thank}\:{you} \\ $$
