Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 138580 by Bekzod Jumayev last updated on 15/Apr/21

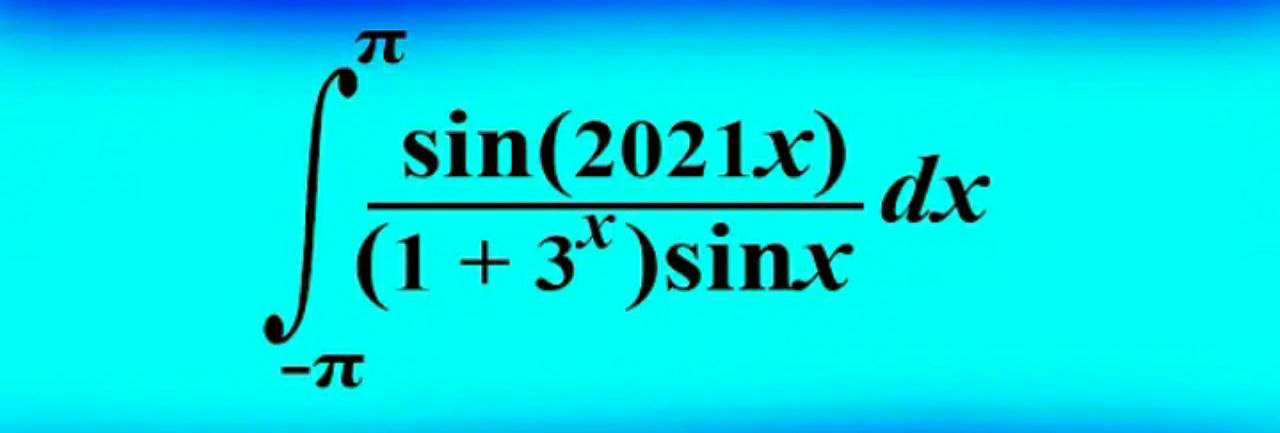
Commented by Bekzod Jumayev last updated on 15/Apr/21

Please help?

$${Please}\:{help}? \\ $$$$ \\ $$

Answered by Ar Brandon last updated on 15/Apr/21

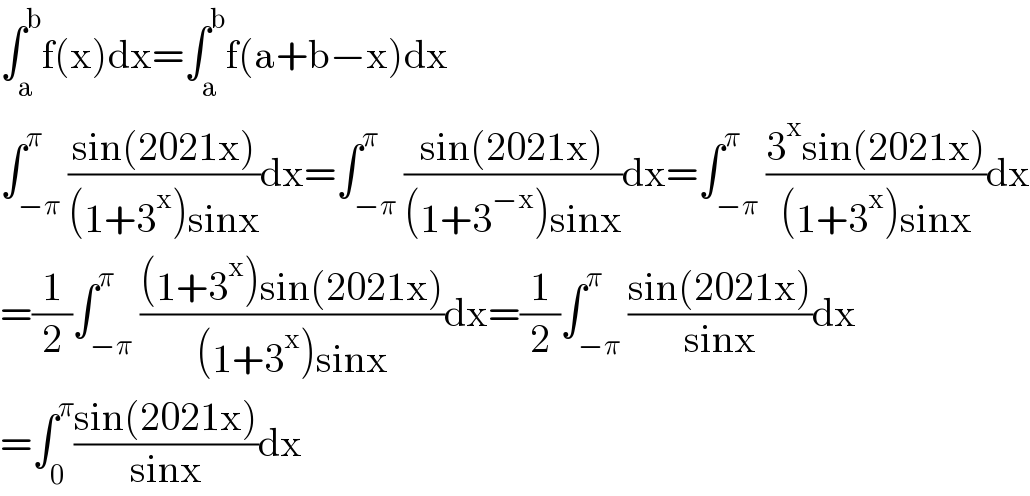
∫_a ^b f(x)dx=∫_a ^b f(a+b−x)dx ∫_(−π) ^π ((sin(2021x))/((1+3^x )sinx))dx=∫_(−π) ^π ((sin(2021x))/((1+3^(−x) )sinx))dx=∫_(−π) ^π ((3^x sin(2021x))/((1+3^x )sinx))dx =(1/2)∫_(−π) ^π (((1+3^x )sin(2021x))/((1+3^x )sinx))dx=(1/2)∫_(−π) ^π ((sin(2021x))/(sinx))dx =∫_0 ^π ((sin(2021x))/(sinx))dx

$$\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right)\mathrm{dx} \\ $$$$\int_{−\pi} ^{\pi} \frac{\mathrm{sin}\left(\mathrm{2021x}\right)}{\left(\mathrm{1}+\mathrm{3}^{\mathrm{x}} \right)\mathrm{sinx}}\mathrm{dx}=\int_{−\pi} ^{\pi} \frac{\mathrm{sin}\left(\mathrm{2021x}\right)}{\left(\mathrm{1}+\mathrm{3}^{−\mathrm{x}} \right)\mathrm{sinx}}\mathrm{dx}=\int_{−\pi} ^{\pi} \frac{\mathrm{3}^{\mathrm{x}} \mathrm{sin}\left(\mathrm{2021x}\right)}{\left(\mathrm{1}+\mathrm{3}^{\mathrm{x}} \right)\mathrm{sinx}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\pi} ^{\pi} \frac{\left(\mathrm{1}+\mathrm{3}^{\mathrm{x}} \right)\mathrm{sin}\left(\mathrm{2021x}\right)}{\left(\mathrm{1}+\mathrm{3}^{\mathrm{x}} \right)\mathrm{sinx}}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\pi} ^{\pi} \frac{\mathrm{sin}\left(\mathrm{2021x}\right)}{\mathrm{sinx}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sin}\left(\mathrm{2021x}\right)}{\mathrm{sinx}}\mathrm{dx} \\ $$

Answered by phanphuoc last updated on 15/Apr/21

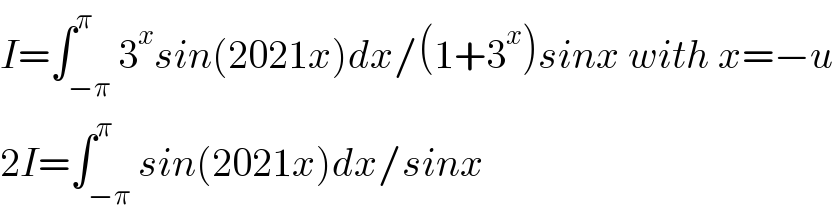
I=∫_(−π) ^π 3^x sin(2021x)dx/(1+3^x )sinx with x=−u 2I=∫_(−π) ^π sin(2021x)dx/sinx

$${I}=\int_{−\pi} ^{\pi} \mathrm{3}^{{x}} {sin}\left(\mathrm{2021}{x}\right){dx}/\left(\mathrm{1}+\mathrm{3}^{{x}} \right){sinx}\:{with}\:{x}=−{u} \\ $$$$\mathrm{2}{I}=\int_{−\pi} ^{\pi} {sin}\left(\mathrm{2021}{x}\right){dx}/{sinx} \\ $$

Answered by mnjuly1970 last updated on 15/Apr/21

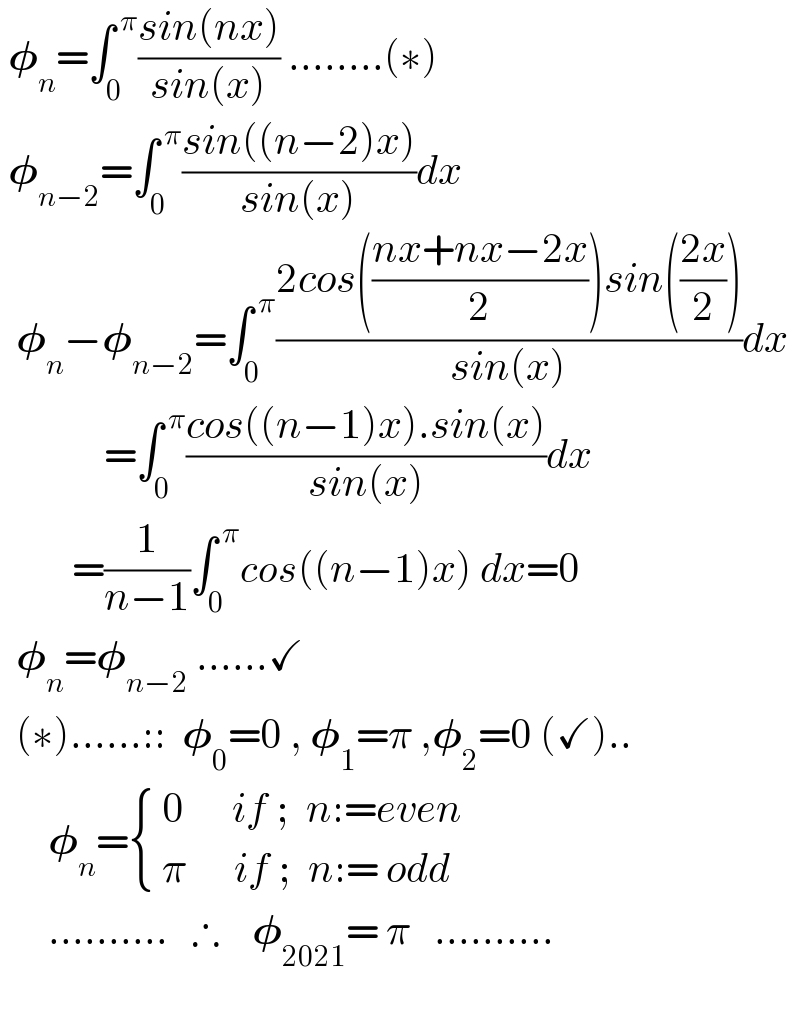
𝛗_n =∫_0 ^( π) ((sin(nx))/(sin(x))) ........(∗) 𝛗_(n−2) =∫_0 ^( π) ((sin((n−2)x))/(sin(x)))dx 𝛗_n −𝛗_(n−2) =∫_0 ^( π) ((2cos(((nx+nx−2x)/2))sin(((2x)/2)))/(sin(x)))dx =∫_0 ^( π) ((cos((n−1)x).sin(x))/(sin(x)))dx =(1/(n−1))∫_0 ^( π) cos((n−1)x) dx=0 𝛗_n =𝛗_(n−2) ......✓ (∗)......:: 𝛗_0 =0 , 𝛗_1 =π ,𝛗_2 =0 (✓).. 𝛗_n = { (( 0 if ; n:=even)),(( π if ; n:= odd )) :} .......... ∴ 𝛗_(2021) = π ..........

$$\:\boldsymbol{\phi}_{{n}} =\int_{\mathrm{0}} ^{\:\pi} \frac{{sin}\left({nx}\right)}{{sin}\left({x}\right)}\:........\left(\ast\right) \\ $$$$\:\boldsymbol{\phi}_{{n}−\mathrm{2}} =\int_{\mathrm{0}} ^{\:\pi} \frac{{sin}\left(\left({n}−\mathrm{2}\right){x}\right)}{{sin}\left({x}\right)}{dx} \\ $$$$\:\:\boldsymbol{\phi}_{{n}} −\boldsymbol{\phi}_{{n}−\mathrm{2}} =\int_{\mathrm{0}} ^{\:\pi} \frac{\mathrm{2}{cos}\left(\frac{{nx}+{nx}−\mathrm{2}{x}}{\mathrm{2}}\right){sin}\left(\frac{\mathrm{2}{x}}{\mathrm{2}}\right)}{{sin}\left({x}\right)}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\:\pi} \frac{{cos}\left(\left({n}−\mathrm{1}\right){x}\right).{sin}\left({x}\right)}{{sin}\left({x}\right)}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{n}−\mathrm{1}}\int_{\mathrm{0}} ^{\:\pi} {cos}\left(\left({n}−\mathrm{1}\right){x}\right)\:{dx}=\mathrm{0} \\ $$$$\:\:\boldsymbol{\phi}_{{n}} =\boldsymbol{\phi}_{{n}−\mathrm{2}} \:......\checkmark \\ $$$$\:\:\left(\ast\right)......::\:\:\boldsymbol{\phi}_{\mathrm{0}} =\mathrm{0}\:,\:\boldsymbol{\phi}_{\mathrm{1}} =\pi\:,\boldsymbol{\phi}_{\mathrm{2}} =\mathrm{0}\:\left(\checkmark\right).. \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}_{{n}} =\begin{cases}{\:\mathrm{0}\:\:\:\:\:\:{if}\:;\:\:{n}:={even}}\\{\:\pi\:\:\:\:\:\:{if}\:;\:\:{n}:=\:{odd}\:\:}\end{cases} \\ $$$$\:\:\:\:\:\:..........\:\:\:\therefore\:\:\:\:\boldsymbol{\phi}_{\mathrm{2021}} =\:\pi\:\:\:.......... \\ $$$$\:\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com