
Question Number 138554 by cherokeesay last updated on 14/Apr/21
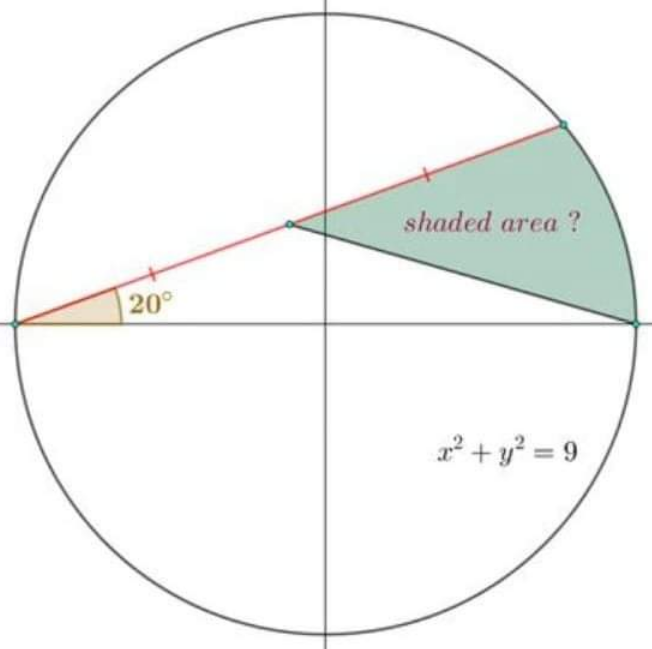
Answered by mr W last updated on 14/Apr/21
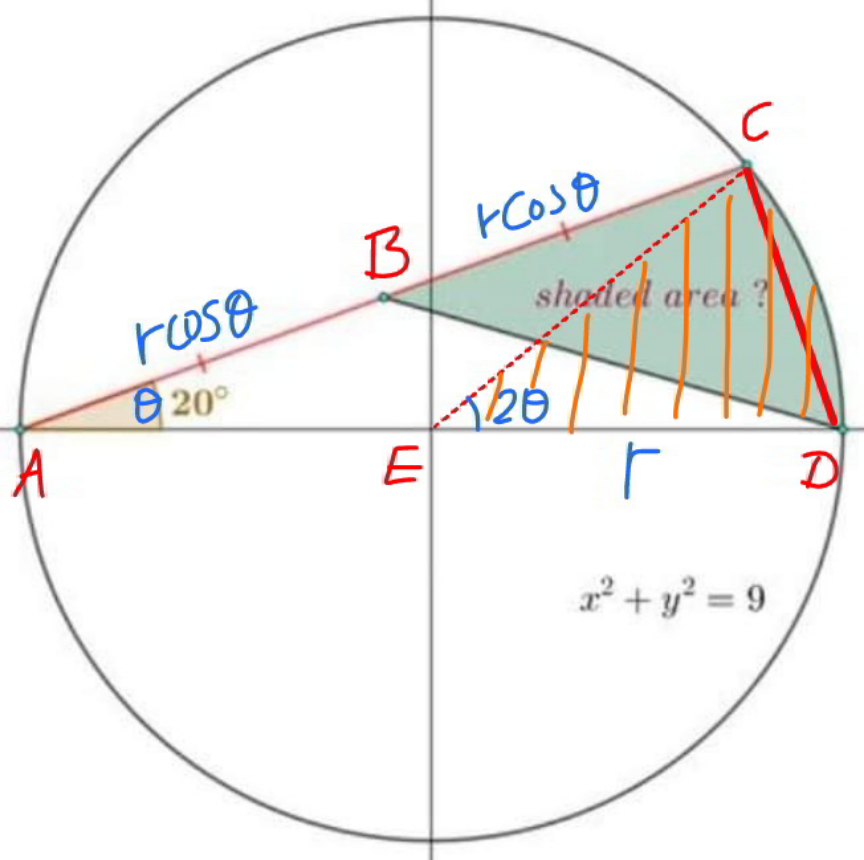
Commented by mr W last updated on 14/Apr/21
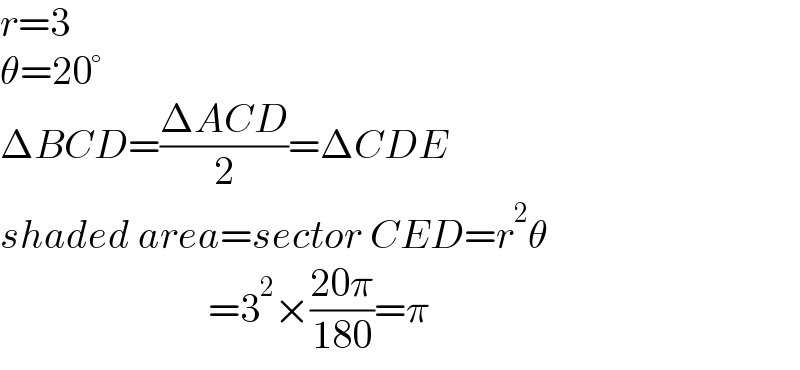
$${r}=\mathrm{3} \\ $$$$\theta=\mathrm{20}° \\ $$$$\Delta{BCD}=\frac{\Delta{ACD}}{\mathrm{2}}=\Delta{CDE} \\ $$$${shaded}\:{area}={sector}\:{CED}={r}^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}^{\mathrm{2}} ×\frac{\mathrm{20}\pi}{\mathrm{180}}=\pi \\ $$
Commented by cherokeesay last updated on 14/Apr/21
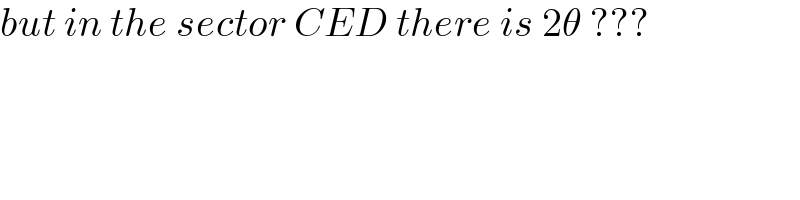
$${but}\:{in}\:{the}\:{sector}\:{CED}\:{there}\:{is}\:\mathrm{2}\theta\:??? \\ $$$$ \\ $$
Commented by mr W last updated on 15/Apr/21
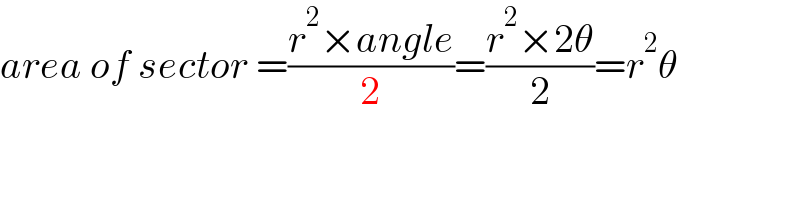
$${area}\:{of}\:{sector}\:=\frac{{r}^{\mathrm{2}} ×{angle}}{\mathrm{2}}=\frac{{r}^{\mathrm{2}} ×\mathrm{2}\theta}{\mathrm{2}}={r}^{\mathrm{2}} \theta \\ $$
Commented by cherokeesay last updated on 15/Apr/21

$${thanks} \\ $$
