Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 13835 by Tinkutara last updated on 24/May/17

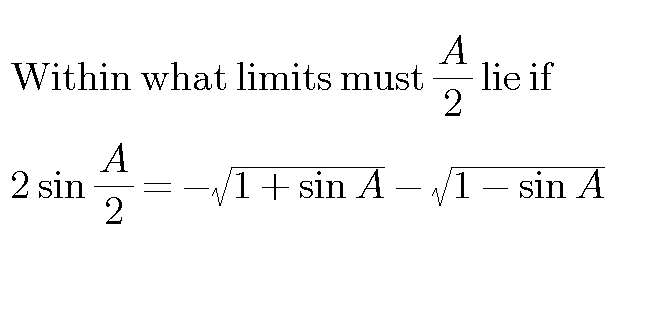
Commented by Tinkutara last updated on 24/May/17

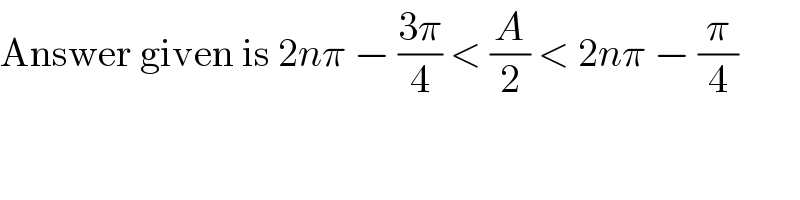
Answer given is 2nπ − ((3π)/4) < (A/2) < 2nπ − (π/4)

$$\mathrm{Answer}\:\mathrm{given}\:\mathrm{is}\:\mathrm{2}{n}\pi\:−\:\frac{\mathrm{3}\pi}{\mathrm{4}}\:<\:\frac{{A}}{\mathrm{2}}\:<\:\mathrm{2}{n}\pi\:−\:\frac{\pi}{\mathrm{4}} \\ $$

Answered by ajfour last updated on 24/May/17

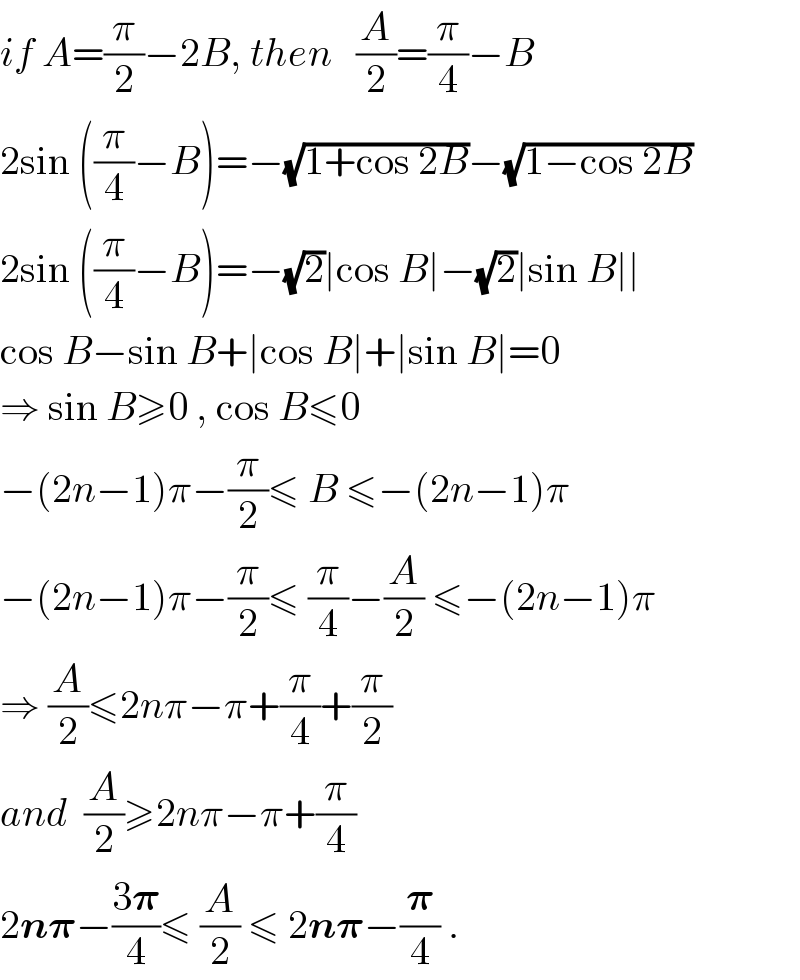
if A=(π/2)−2B, then (A/2)=(π/4)−B 2sin ((π/4)−B)=−(√(1+cos 2B))−(√(1−cos 2B)) 2sin ((π/4)−B)=−(√2)∣cos B∣−(√2)∣sin B∣∣ cos B−sin B+∣cos B∣+∣sin B∣=0 ⇒ sin B≥0 , cos B≤0 −(2n−1)π−(π/2)≤ B ≤−(2n−1)π −(2n−1)π−(π/2)≤ (π/4)−(A/2) ≤−(2n−1)π ⇒ (A/2)≤2nπ−π+(π/4)+(π/2) and (A/2)≥2nπ−π+(π/4) 2n𝛑−((3𝛑)/4)≤ (A/2) ≤ 2n𝛑−(𝛑/4) .

$${if}\:{A}=\frac{\pi}{\mathrm{2}}−\mathrm{2}{B},\:{then}\:\:\:\frac{{A}}{\mathrm{2}}=\frac{\pi}{\mathrm{4}}−{B} \\ $$$$\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{4}}−{B}\right)=−\sqrt{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{B}}−\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{B}} \\ $$$$\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{4}}−{B}\right)=−\sqrt{\mathrm{2}}\mid\mathrm{cos}\:{B}\mid−\sqrt{\mathrm{2}}\mid\mathrm{sin}\:{B}\mid\mid \\ $$$$\mathrm{cos}\:{B}−\mathrm{sin}\:{B}+\mid\mathrm{cos}\:{B}\mid+\mid\mathrm{sin}\:{B}\mid=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{sin}\:{B}\geqslant\mathrm{0}\:,\:\mathrm{cos}\:{B}\leqslant\mathrm{0} \\ $$$$−\left(\mathrm{2}{n}−\mathrm{1}\right)\pi−\frac{\pi}{\mathrm{2}}\leqslant\:{B}\:\leqslant−\left(\mathrm{2}{n}−\mathrm{1}\right)\pi \\ $$$$−\left(\mathrm{2}{n}−\mathrm{1}\right)\pi−\frac{\pi}{\mathrm{2}}\leqslant\:\frac{\pi}{\mathrm{4}}−\frac{{A}}{\mathrm{2}}\:\leqslant−\left(\mathrm{2}{n}−\mathrm{1}\right)\pi \\ $$$$\Rightarrow\:\frac{{A}}{\mathrm{2}}\leqslant\mathrm{2}{n}\pi−\pi+\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{2}} \\ $$$${and}\:\:\frac{{A}}{\mathrm{2}}\geqslant\mathrm{2}{n}\pi−\pi+\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{2}\boldsymbol{{n}\pi}−\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}\leqslant\:\frac{{A}}{\mathrm{2}}\:\leqslant\:\mathrm{2}\boldsymbol{{n}\pi}−\frac{\boldsymbol{\pi}}{\mathrm{4}}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com