
Question Number 138175 by ajfour last updated on 10/Apr/21
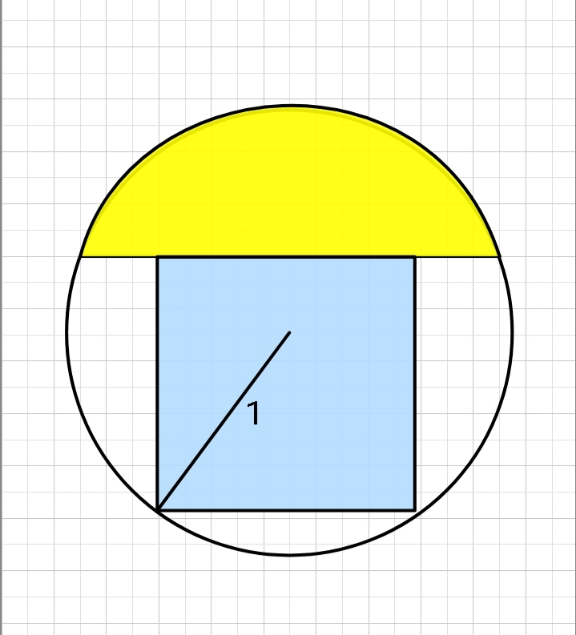
Commented by ajfour last updated on 10/Apr/21

$${If}\:{the}\:{yellow}\:{and}\:{blue}\:{areas}\:{are} \\ $$$${equal},\:{find}\:{edge}\:{length}\:{of}\:{the} \\ $$$${blue}\:{square}.\:\left({radius}\:{of}\:{circle}=\mathrm{1}\right) \\ $$
Answered by mr W last updated on 10/Apr/21
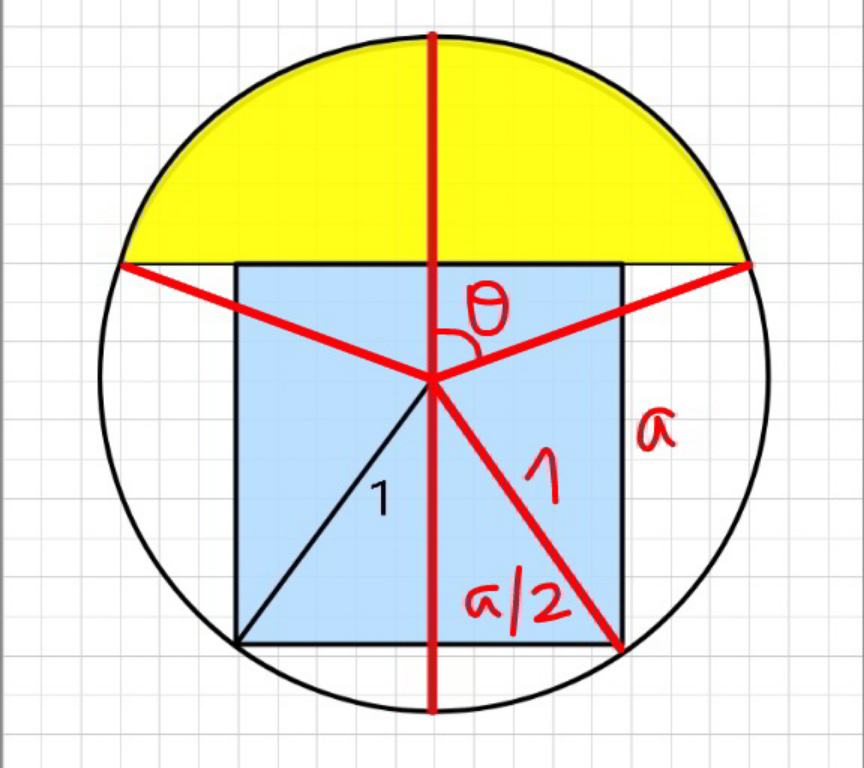
Commented by mr W last updated on 11/Apr/21
$${please}\:{sir}!\:{i}\:{found}\:{no}\:{better}\:{way}\:{to} \\ $$$${solve}. \\ $$
Commented by mr W last updated on 11/Apr/21

$${yellow}\:{segment}\:{area}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\theta−\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\theta−\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta \\ $$$${blue}\:{square}\:\:{area}={a}^{\mathrm{2}} \\ $$$$\theta−\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta={a}^{\mathrm{2}} \\ $$$$\Rightarrow{a}=\sqrt{\theta−\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta} \\ $$$$ \\ $$$$\sqrt{\mathrm{1}^{\mathrm{2}} −\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} }+\mathrm{1}×\mathrm{cos}\:\theta={a} \\ $$$$\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }+\mathrm{2cos}\:\theta=\mathrm{2}{a} \\ $$$$\Rightarrow\sqrt{\mathrm{4}−\theta+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}+\mathrm{2cos}\:\theta=\mathrm{2}\sqrt{\theta−\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\theta\approx\mathrm{1}.\mathrm{3496}\:\left(=\mathrm{77}.\mathrm{326}°\right) \\ $$$$\Rightarrow{a}\approx\mathrm{1}.\mathrm{0656} \\ $$
Commented by ajfour last updated on 11/Apr/21

$${Thank}\:{you}\:{sir},\:{the}\:{previous} \\ $$$${cube}-{cylinder}\:{question}\:{i}\:{will} \\ $$$${attempt}\:{again}\:{sir},\:{to}\:{match}\:{with}\:{your}\:{solution}. \\ $$
