Question and Answers Forum

All Questions      Topic List

Vector Calculus Questions

Previous in All Question      Next in All Question      

Previous in Vector Calculus      Next in Vector Calculus      

Question Number 137627 by rs4089 last updated on 04/Apr/21

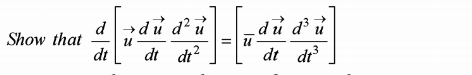
Answered by MrGaster last updated on 16/Feb/25

Prove:(d/dt)[u^→ (du^→ /dt)]=u^→ (d^2 u^→ /dt^2 )+(du^→ /dt) (du^→ /dt) (d/dt)[u^→ (du^→ /dt)]=u^→ (d^2 u^→ /dt^2 )+((du^→ /dt))^2 (d/dt)[u^→ (du^→ /dt) (d^2 u/dt^2 )]=(d/dt)[u^→ (d^2 u^→ /dt^2 )](du^→ /dt)+u^→ (d/dt)[(du^→ /dt) (d^2 u^→ /dt^2 )] (d/dt)[u^→ (d^2 u^→ /dt^2 )]=u^→ (d^3 u^→ /dt^3 )+(du^→ /dt) (d^2 u^→ /dt^2 ) (d/dt)[u^→ (du^→ /dt) (d^2 u^→ /dt^2 )]=(u^→ (d^3 u^→ /dt^3 )+(du^→ /dt) (d^2 u^→ /dt^2 ))(du^→ /dt)+u^→ (d/dt)[(du^→ /dt) (d^2 u^→ /dt^2 )] (d/dt)[(du^→ /dt) (d^2 u^→ /dt^2 )]=(d^2 u^→ /dt) (d^2 u^→ /dt^2 )+(du^→ /dt) (d^3 u^→ /dt^3 ) =u^→ (du^→ /dt) (d^3 u^→ /dt)+((du^→ /dt))^2 =(d^2 u^→ /dt^2 )+u^→ (d^2 u^→ /dt^2 ) (d^2 u^→ /dt^2 ) determinant ((((d/dt)[u^→ (du^→ /dt) (d^2 u^→ /dt^2 )]=[u^_ (du^→ /dt) (d^3 u^→ /dt^3 )])),(((d/dt)[u(du^→ /dt) (d^2 u^→ /dt^2 )]=[u(du^→ /dt) (d^3 u^→ /dt^3 )])))

$$ \\ $$$$\mathrm{Prove}:\frac{{d}}{{dt}}\left[\overset{\rightarrow} {{u}}\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\right]=\overset{\rightarrow} {{u}}\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }+\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}\overset{\rightarrow} {{u}}}{{dt}} \\ $$$$\frac{{d}}{{dt}}\left[\overset{\rightarrow} {{u}}\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\right]=\overset{\rightarrow} {{u}}\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }+\left(\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\right)^{\mathrm{2}} \\ $$$$\frac{{d}}{{dt}}\left[\overset{\rightarrow} {{u}}\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{2}} {u}}{{dt}^{\mathrm{2}} }\right]=\frac{{d}}{{dt}}\left[\overset{\rightarrow} {{u}}\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }\right]\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}+\overset{\rightarrow} {{u}}\frac{{d}}{{dt}}\left[\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }\right] \\ $$$$\frac{{d}}{{dt}}\left[\overset{\rightarrow} {{u}}\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }\right]=\overset{\rightarrow} {{u}}\frac{{d}^{\mathrm{3}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{3}} }+\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} } \\ $$$$\frac{{d}}{{dt}}\left[\overset{\rightarrow} {{u}}\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }\right]=\left(\overset{\rightarrow} {{u}}\frac{{d}^{\mathrm{3}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{3}} }+\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }\right)\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}+\overset{\rightarrow} {{u}}\frac{{d}}{{dt}}\left[\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }\right] \\ $$$$\frac{{d}}{{dt}}\left[\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }\right]=\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }+\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{3}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{3}} } \\ $$$$=\overset{\rightarrow} {{u}}\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{3}} \overset{\rightarrow} {{u}}}{{dt}}+\left(\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\right)^{\mathrm{2}} =\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }+\overset{\rightarrow} {{u}}\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }\:\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} } \\ $$$$\begin{matrix}{\frac{{d}}{{dt}}\left[\overset{\rightarrow} {{u}}\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }\right]=\left[\overset{\_} {{u}}\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{3}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{3}} }\right]}\\{\frac{{d}}{{dt}}\left[{u}\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{2}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{2}} }\right]=\left[{u}\frac{{d}\overset{\rightarrow} {{u}}}{{dt}}\:\frac{{d}^{\mathrm{3}} \overset{\rightarrow} {{u}}}{{dt}^{\mathrm{3}} }\right]}\end{matrix} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com