
Question Number 137007 by SLVR last updated on 28/Mar/21

Commented by SLVR last updated on 28/Mar/21
$${kindly}\:{send}\:{me}\:{the}\:{solution} \\ $$
Commented by mr W last updated on 28/Mar/21
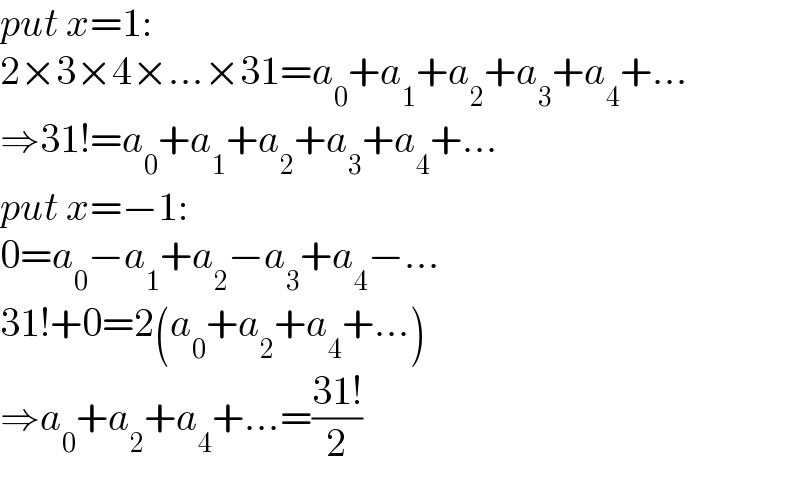
$${put}\:{x}=\mathrm{1}: \\ $$$$\mathrm{2}×\mathrm{3}×\mathrm{4}×...×\mathrm{31}={a}_{\mathrm{0}} +{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +{a}_{\mathrm{3}} +{a}_{\mathrm{4}} +... \\ $$$$\Rightarrow\mathrm{31}!={a}_{\mathrm{0}} +{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +{a}_{\mathrm{3}} +{a}_{\mathrm{4}} +... \\ $$$${put}\:{x}=−\mathrm{1}: \\ $$$$\mathrm{0}={a}_{\mathrm{0}} −{a}_{\mathrm{1}} +{a}_{\mathrm{2}} −{a}_{\mathrm{3}} +{a}_{\mathrm{4}} −... \\ $$$$\mathrm{31}!+\mathrm{0}=\mathrm{2}\left({a}_{\mathrm{0}} +{a}_{\mathrm{2}} +{a}_{\mathrm{4}} +...\right) \\ $$$$\Rightarrow{a}_{\mathrm{0}} +{a}_{\mathrm{2}} +{a}_{\mathrm{4}} +...=\frac{\mathrm{31}!}{\mathrm{2}} \\ $$
Commented by SLVR last updated on 31/Mar/21

$${thanks}...{Mr}.{W} \\ $$$$ \\ $$
