
Question Number 134949 by rexford last updated on 08/Mar/21

Answered by bobhans last updated on 30/Jan/22
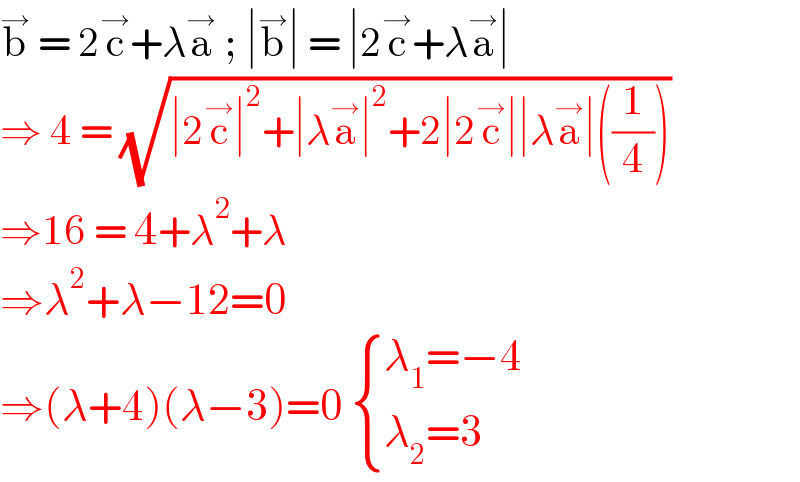
$$\overset{\rightarrow} {\mathrm{b}}\:=\:\mathrm{2}\overset{\rightarrow} {\mathrm{c}}+\lambda\overset{\rightarrow} {\mathrm{a}}\:;\:\mid\overset{\rightarrow} {\mathrm{b}}\mid\:=\:\mid\mathrm{2}\overset{\rightarrow} {\mathrm{c}}+\lambda\overset{\rightarrow} {\mathrm{a}}\mid \\ $$$$\Rightarrow\:\mathrm{4}\:=\:\sqrt{\mid\mathrm{2}\overset{\rightarrow} {\mathrm{c}}\mid^{\mathrm{2}} +\mid\lambda\overset{\rightarrow} {\mathrm{a}}\mid^{\mathrm{2}} +\mathrm{2}\mid\mathrm{2}\overset{\rightarrow} {\mathrm{c}}\mid\mid\lambda\overset{\rightarrow} {\mathrm{a}}\mid\left(\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$$$\Rightarrow\mathrm{16}\:=\:\mathrm{4}+\lambda^{\mathrm{2}} +\lambda\: \\ $$$$\Rightarrow\lambda^{\mathrm{2}} +\lambda−\mathrm{12}=\mathrm{0} \\ $$$$\Rightarrow\left(\lambda+\mathrm{4}\right)\left(\lambda−\mathrm{3}\right)=\mathrm{0}\:\begin{cases}{\lambda_{\mathrm{1}} =−\mathrm{4}}\\{\lambda_{\mathrm{2}} =\mathrm{3}}\end{cases} \\ $$
