
Question Number 134795 by 0731619177 last updated on 07/Mar/21
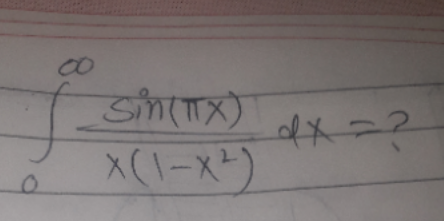
Answered by EDWIN88 last updated on 07/Mar/21

$$\:\mathrm{noting}\:\mathrm{that}\:\mathrm{the}\:\mathrm{integrand}\:\mathrm{is}\:\mathrm{even}\:\mathrm{function} \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}\:\mathrm{dx} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{4}}\int_{−\infty} ^{\infty} \left(\frac{\mathrm{2}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right).\mathrm{sin}\:\left(\pi\mathrm{x}\right)\:\mathrm{dx}\: \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{4}}.\left(\mathrm{2}\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}−\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\mathrm{x}\right)}{\mathrm{x}+\mathrm{1}}\mathrm{dx}−\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\mathrm{x}\right)}{\mathrm{x}−\mathrm{1}}\mathrm{dx}\:\right) \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{4}}.\left(\mathrm{2}\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}−\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\left(\mathrm{x}−\mathrm{1}\right)\right)}{\mathrm{x}}\mathrm{dx}−\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\left(\mathrm{x}+\mathrm{1}\right)\right)}{\mathrm{x}}\mathrm{dx}\right) \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}+\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}+\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\right) \\ $$$$\mathrm{I}=\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\left(\pi\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:.\:\mathrm{let}\:\mathrm{u}\:=\:\pi\mathrm{x}\:\rightarrow\mathrm{x}=\frac{\mathrm{u}}{\pi} \\ $$$$\mathrm{I}=\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\mathrm{u}}{\left(\frac{\mathrm{u}}{\pi}\right)}\:\left(\frac{\mathrm{du}}{\pi}\right)=\int_{−\infty} ^{\infty} \frac{\mathrm{sin}\:\mathrm{u}}{\mathrm{u}}\:\mathrm{du}\:=\:\pi \\ $$
Commented by liberty last updated on 07/Mar/21

$$ \\ $$ausgezeichneter Herr Edwin
Commented by 0731619177 last updated on 07/Mar/21

$$ \\ $$$${tanks} \\ $$
