
Question Number 134604 by mohammad17 last updated on 05/Mar/21
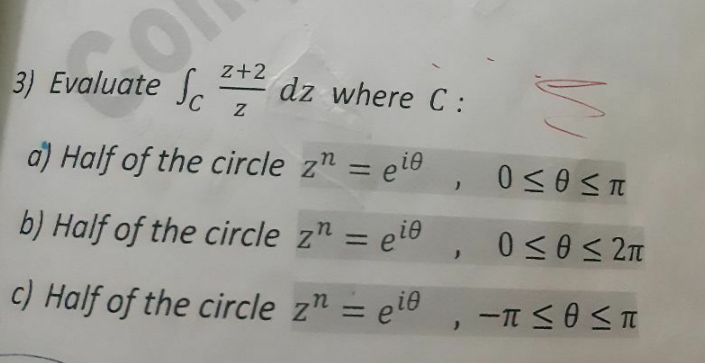
Commented by mohammad17 last updated on 05/Mar/21
$${how}\:{can}\:{solve}\:{this} \\ $$
Commented by mohammad17 last updated on 05/Mar/21

$$??????? \\ $$
Answered by mathmax by abdo last updated on 06/Mar/21
![z^n =e^(iθ ) ⇒z=e^((iθ)/n) and o≤(θ/n)≤(π/n) ∫_C ((z+2)/z)dz =∫_C dz +∫_C (2/z)dz =∫_0 ^π (i/n)e^((iθ)/n) dθ +∫_0 ^π 2 e^(−((iθ)/n)) (i/n)e^((iθ)/n) dθ =(i/n)(n/i)[e^((iθ)/n) ]_0 ^π −(i/n)((2n)/i)[ e^(−((iθ)/n)) ]_0 ^π =e^((iπ)/n) −1 −2(e^(−((iπ)/n)) −1) =e^((iπ)/n) −2e^(−((iπ)/n)) +1](Q134632.png)
$$\mathrm{z}^{\mathrm{n}} \:=\mathrm{e}^{\mathrm{i}\theta\:} \:\Rightarrow\mathrm{z}=\mathrm{e}^{\frac{\mathrm{i}\theta}{\mathrm{n}}} \:\:\mathrm{and}\:\mathrm{o}\leqslant\frac{\theta}{\mathrm{n}}\leqslant\frac{\pi}{\mathrm{n}} \\ $$$$\int_{\mathrm{C}} \frac{\mathrm{z}+\mathrm{2}}{\mathrm{z}}\mathrm{dz}\:=\int_{\mathrm{C}} \mathrm{dz}\:+\int_{\mathrm{C}} \frac{\mathrm{2}}{\mathrm{z}}\mathrm{dz} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{i}}{\mathrm{n}}\mathrm{e}^{\frac{\mathrm{i}\theta}{\mathrm{n}}} \:\mathrm{d}\theta\:\:+\int_{\mathrm{0}} ^{\pi} \:\mathrm{2}\:\mathrm{e}^{−\frac{\mathrm{i}\theta}{\mathrm{n}}} \:\frac{\mathrm{i}}{\mathrm{n}}\mathrm{e}^{\frac{\mathrm{i}\theta}{\mathrm{n}}} \:\mathrm{d}\theta \\ $$$$=\frac{\mathrm{i}}{\mathrm{n}}\frac{\mathrm{n}}{\mathrm{i}}\left[\mathrm{e}^{\frac{\mathrm{i}\theta}{\mathrm{n}}} \right]_{\mathrm{0}} ^{\pi} \:\:\:−\frac{\mathrm{i}}{\mathrm{n}}\frac{\mathrm{2n}}{\mathrm{i}}\left[\:\mathrm{e}^{−\frac{\mathrm{i}\theta}{\mathrm{n}}} \right]_{\mathrm{0}} ^{\pi} \\ $$$$=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{n}}} −\mathrm{1}\:−\mathrm{2}\left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{n}}} −\mathrm{1}\right)\:=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{n}}} −\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{n}}} \:+\mathrm{1} \\ $$
Commented by mohammad17 last updated on 06/Mar/21
$${thank}\:{you}\:{sir}\:{can}\:{you}\:{solve}\:{all}\:{questio}\:{please} \\ $$
