Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 134511 by mohammad17 last updated on 04/Mar/21

Commented by mohammad17 last updated on 04/Mar/21

how can solve this

$${how}\:{can}\:{solve}\:{this} \\ $$

Commented by mohammad17 last updated on 04/Mar/21

??????

$$?????? \\ $$

Commented by mohammad17 last updated on 04/Mar/21

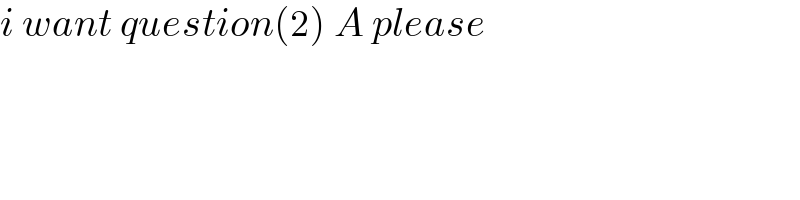
i want question(2) A please

$${i}\:{want}\:{question}\left(\mathrm{2}\right)\:{A}\:{please} \\ $$

Commented by mr W last updated on 04/Mar/21

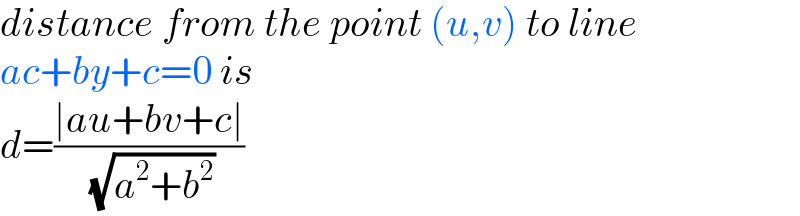
distance from the point (u,v) to line ac+by+c=0 is d=((∣au+bv+c∣)/( (√(a^2 +b^2 ))))

$${distance}\:{from}\:{the}\:{point}\:\left({u},{v}\right)\:{to}\:{line} \\ $$$${ac}+{by}+{c}=\mathrm{0}\:{is} \\ $$$${d}=\frac{\mid{au}+{bv}+{c}\mid}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$

Commented by Dwaipayan Shikari last updated on 06/Mar/21

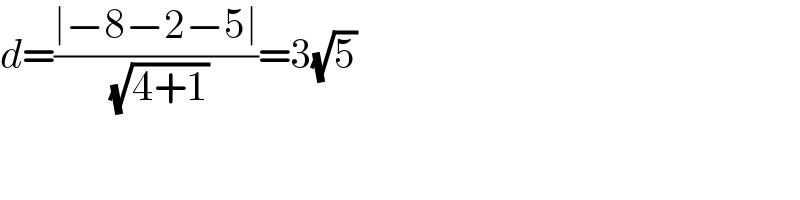
d=((∣−8−2−5∣)/( (√(4+1))))=3(√5)

$${d}=\frac{\mid−\mathrm{8}−\mathrm{2}−\mathrm{5}\mid}{\:\sqrt{\mathrm{4}+\mathrm{1}}}=\mathrm{3}\sqrt{\mathrm{5}} \\ $$

Answered by mathmax by abdo last updated on 06/Mar/21

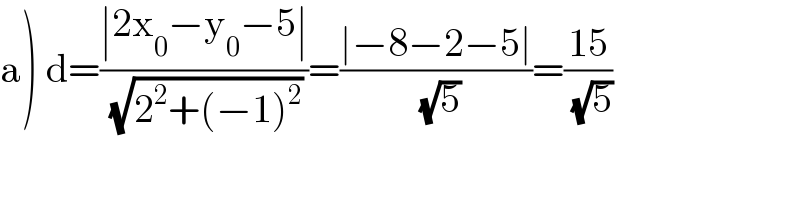
a) d=((∣2x_0 −y_0 −5∣)/( (√(2^2 +(−1)^2 ))))=((∣−8−2−5∣)/( (√5)))=((15)/( (√5)))

$$\left.\mathrm{a}\right)\:\mathrm{d}=\frac{\mid\mathrm{2x}_{\mathrm{0}} −\mathrm{y}_{\mathrm{0}} −\mathrm{5}\mid}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\left(−\mathrm{1}\right)^{\mathrm{2}} }}=\frac{\mid−\mathrm{8}−\mathrm{2}−\mathrm{5}\mid}{\:\sqrt{\mathrm{5}}}=\frac{\mathrm{15}}{\:\sqrt{\mathrm{5}}} \\ $$

Answered by mathmax by abdo last updated on 06/Mar/21

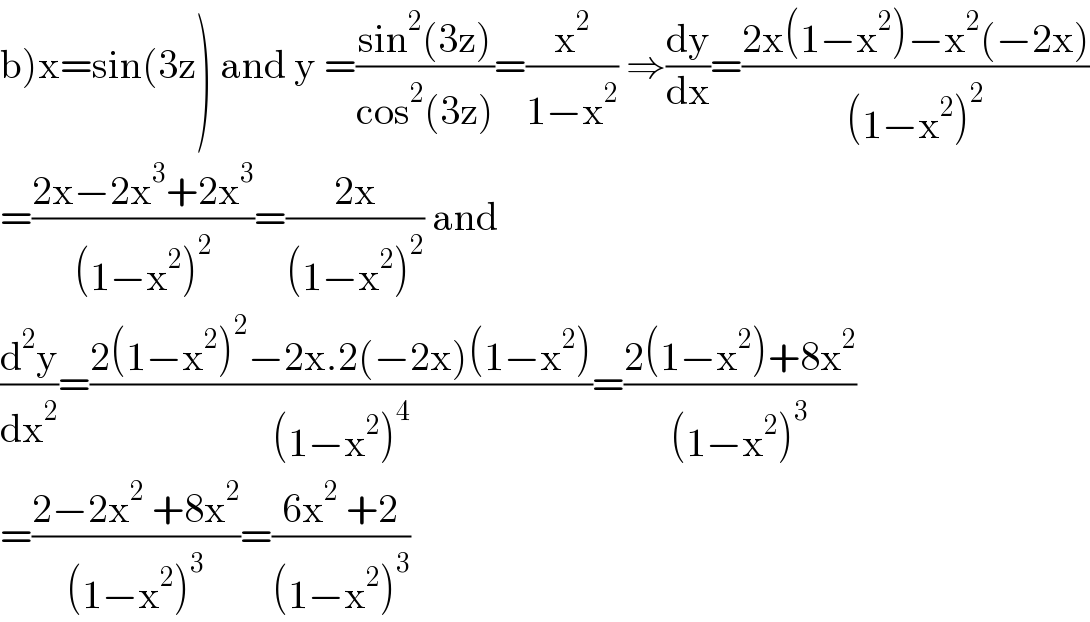
b)x=sin(3z) and y =((sin^2 (3z))/(cos^2 (3z)))=(x^2 /(1−x^2 )) ⇒(dy/dx)=((2x(1−x^2 )−x^2 (−2x))/((1−x^2 )^2 )) =((2x−2x^3 +2x^3 )/((1−x^2 )^2 ))=((2x)/((1−x^2 )^2 )) and (d^2 y/dx^2 )=((2(1−x^2 )^2 −2x.2(−2x)(1−x^2 ))/((1−x^2 )^4 ))=((2(1−x^2 )+8x^2 )/((1−x^2 )^3 )) =((2−2x^2 +8x^2 )/((1−x^2 )^3 ))=((6x^2 +2)/((1−x^2 )^3 ))

$$\left.\mathrm{b}\right)\mathrm{x}=\mathrm{sin}\left(\mathrm{3z}\right)\:\mathrm{and}\:\mathrm{y}\:=\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3z}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{3z}\right)}=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{2x}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)−\mathrm{x}^{\mathrm{2}} \left(−\mathrm{2x}\right)}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2x}−\mathrm{2x}^{\mathrm{3}} +\mathrm{2x}^{\mathrm{3}} }{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{2x}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\mathrm{and} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2x}.\mathrm{2}\left(−\mathrm{2x}\right)\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{4}} }=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)+\mathrm{8x}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{2}−\mathrm{2x}^{\mathrm{2}} \:+\mathrm{8x}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }=\frac{\mathrm{6x}^{\mathrm{2}} \:+\mathrm{2}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com