
Question Number 134482 by benjo_mathlover last updated on 04/Mar/21

$$ \\ $$ How many ways can this be done if you distribute 25 identical pieces of candy among five children?\\n
Commented bymr W last updated on 04/Mar/21

$${you}'{ll}\:{get}\:{problem}\:{if}\:{you}\:{don}'{t}\:{give} \\ $$ $$\left.{each}\:{child}\:\mathrm{5}\:{pieces}!\::\right) \\ $$ $$ \\ $$ $${mathematically}\:{to}\:{get}\:{an}\:{unique} \\ $$ $${answer}\:{you}\:{must}\:{specify}\:{if}\:{each} \\ $$ $${child}\:{may}\:{get}\:{nothing}\:{or}\:{must}\:{get} \\ $$ $${at}\:{least}\:{one}\:{piece}.\:{if}\:{i}\:{were}\:{you},\:{i}'{ll} \\ $$ $${add}\color{mathred}{\:}{\color{mathred}{i}\color{mathred}{f}}\color{mathred}{\:}{\color{mathred}{e}\color{mathred}{a}\color{mathred}{c}\color{mathred}{h}}\color{mathred}{\:}{\color{mathred}{c}\color{mathred}{h}\color{mathred}{i}\color{mathred}{l}\color{mathred}{d}}\color{mathred}{\:}{\color{mathred}{m}\color{mathred}{u}\color{mathred}{s}\color{mathred}{t}}\color{mathred}{\:}{\color{mathred}{g}\color{mathred}{e}\color{mathred}{t}}\color{mathred}{\:}{\color{mathred}{a}\color{mathred}{t}}\color{mathred}{\:}{\color{mathred}{l}\color{mathred}{e}\color{mathred}{a}\color{mathred}{s}\color{mathred}{t}} \\ $$ $${\color{mathred}{t}\color{mathred}{w}\color{mathred}{o}}\color{mathred}{\:}{\color{mathred}{p}\color{mathred}{i}\color{mathred}{e}\color{mathred}{c}\color{mathred}{e}\color{mathred}{s}}. \\ $$
Commented bybenjo_mathlover last updated on 04/Mar/21

$$ \\ $$ hello sir, that's the problem written in the book no other explanation\\n
Commented bymr W last updated on 04/Mar/21
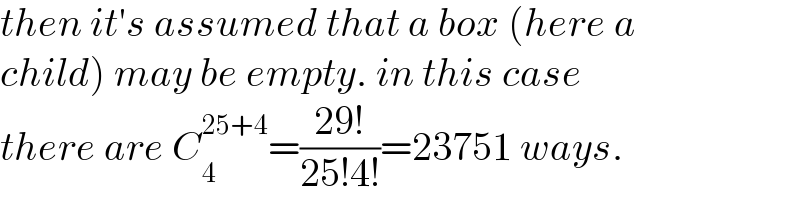
$${then}\:{it}'{s}\:{assumed}\:{that}\:{a}\:{box}\:\left({here}\:{a}\right. \\ $$ $$\left.{child}\right)\:{may}\:{be}\:{empty}.\:{in}\:{this}\:{case} \\ $$ $${there}\:{are}\:{C}_{\mathrm{4}} ^{\mathrm{25}+\mathrm{4}} =\frac{\mathrm{29}!}{\mathrm{25}!\mathrm{4}!}=\mathrm{23751}\:{ways}. \\ $$
Commented bymr W last updated on 04/Mar/21

$${\color{mathred}{i}\color{mathred}{f}}\color{mathred}{\:}{\color{mathred}{e}\color{mathred}{a}\color{mathred}{c}\color{mathred}{h}}\color{mathred}{\:}{\color{mathred}{c}\color{mathred}{h}\color{mathred}{i}\color{mathred}{l}\color{mathred}{d}}\color{mathred}{\:}{\color{mathred}{m}\color{mathred}{u}\color{mathred}{s}\color{mathred}{t}}\color{mathred}{\:}{\color{mathred}{g}\color{mathred}{e}\color{mathred}{t}}\color{mathred}{\:}{\color{mathred}{a}\color{mathred}{t}}\color{mathred}{\:}{\color{mathred}{l}\color{mathred}{e}\color{mathred}{a}\color{mathred}{s}\color{mathred}{t}} \\ $$ $${\color{mathred}{t}\color{mathred}{w}\color{mathred}{o}}\color{mathred}{\:}{\color{mathred}{p}\color{mathred}{i}\color{mathred}{e}\color{mathred}{c}\color{mathred}{e}\color{mathred}{s}},\:{then}\:{we}\:{have}\:{in}\:{fact}\:{only} \\ $$ $$\mathrm{15}\:{pieces}\:{to}\:{distribute},\:{there}\:{are} \\ $$ $${C}_{\mathrm{4}} ^{\mathrm{15}+\mathrm{4}} =\mathrm{3876}\:{ways}. \\ $$
Commented bybenjo_mathlover last updated on 04/Mar/21

$$\mathrm{ok}\:\mathrm{sir}.\:\mathrm{thanks} \\ $$
