
Question Number 134037 by benjo_mathlover last updated on 26/Feb/21
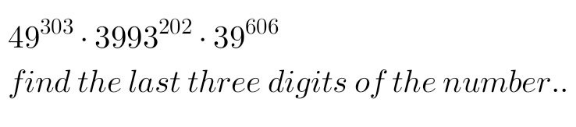
Answered by john_santu last updated on 27/Feb/21
![49^(303) .3993^(202) .39^(606) = (7^2 )^(303) . 3^(606) .13^(606) .3^(202) .11^(606) = (7×13×11)^(606) . 3^(808) = 1001^(606) .(3^(200) )^4 .3^8 [ note by 3^(400) ≡ 1 mod 1000 ] ≡ 1×1×3^8 (mod 1000) ≡ 6561 (mod 1000) ≡ 561 (mod 1000). Hence it′s the last three digits are 561.](Q134057.png)
$$\mathrm{49}^{\mathrm{303}} .\mathrm{3993}^{\mathrm{202}} .\mathrm{39}^{\mathrm{606}} \:= \\ $$$$\left(\mathrm{7}^{\mathrm{2}} \right)^{\mathrm{303}} .\:\mathrm{3}^{\mathrm{606}} .\mathrm{13}^{\mathrm{606}} \:.\mathrm{3}^{\mathrm{202}} .\mathrm{11}^{\mathrm{606}} \:= \\ $$$$\left(\mathrm{7}×\mathrm{13}×\mathrm{11}\right)^{\mathrm{606}} .\:\mathrm{3}^{\mathrm{808}} \:= \\ $$$$\mathrm{1001}^{\mathrm{606}} \:.\left(\mathrm{3}^{\mathrm{200}} \right)^{\mathrm{4}} .\mathrm{3}^{\mathrm{8}} \: \\ $$$$\left[\:{note}\:{by}\:\mathrm{3}^{\mathrm{400}} \:\equiv\:\mathrm{1}\:{mod}\:\mathrm{1000}\:\right] \\ $$$$\equiv\:\mathrm{1}×\mathrm{1}×\mathrm{3}^{\mathrm{8}} \:\left({mod}\:\mathrm{1000}\right) \\ $$$$\equiv\:\mathrm{6561}\:\left({mod}\:\mathrm{1000}\right) \\ $$$$\equiv\:\mathrm{561}\:\left({mod}\:\mathrm{1000}\right). \\ $$$${Hence}\:{it}'{s}\:{the}\:{last}\:{three}\:{digits} \\ $$$${are}\:\mathrm{561}.\: \\ $$
