
Question Number 133961 by Ahmed1hamouda last updated on 25/Feb/21
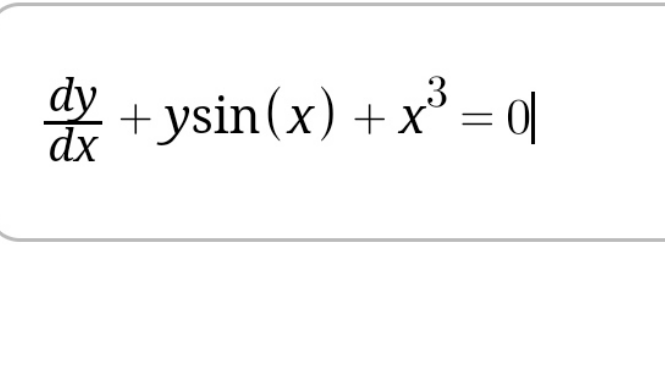
Answered by mathmax by abdo last updated on 27/Feb/21
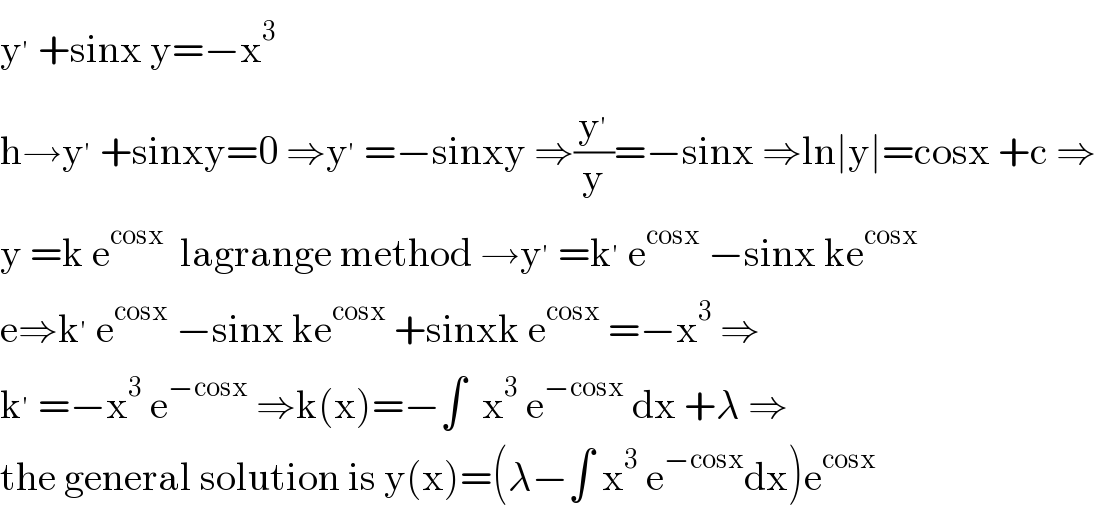
$$\mathrm{y}^{'} \:+\mathrm{sinx}\:\mathrm{y}=−\mathrm{x}^{\mathrm{3}} \\ $$$$\mathrm{h}\rightarrow\mathrm{y}^{'} \:+\mathrm{sinxy}=\mathrm{0}\:\Rightarrow\mathrm{y}^{'} \:=−\mathrm{sinxy}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}=−\mathrm{sinx}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid=\mathrm{cosx}\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\:=\mathrm{k}\:\mathrm{e}^{\mathrm{cosx}} \:\:\mathrm{lagrange}\:\mathrm{method}\:\rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} \:\mathrm{e}^{\mathrm{cosx}} \:−\mathrm{sinx}\:\mathrm{ke}^{\mathrm{cosx}} \\ $$$$\mathrm{e}\Rightarrow\mathrm{k}^{'} \:\mathrm{e}^{\mathrm{cosx}} \:−\mathrm{sinx}\:\mathrm{ke}^{\mathrm{cosx}} \:+\mathrm{sinxk}\:\mathrm{e}^{\mathrm{cosx}} \:=−\mathrm{x}^{\mathrm{3}} \:\Rightarrow \\ $$$$\mathrm{k}^{'} \:=−\mathrm{x}^{\mathrm{3}} \:\mathrm{e}^{−\mathrm{cosx}} \:\Rightarrow\mathrm{k}\left(\mathrm{x}\right)=−\int\:\:\mathrm{x}^{\mathrm{3}} \:\mathrm{e}^{−\mathrm{cosx}} \:\mathrm{dx}\:+\lambda\:\Rightarrow \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\left(\mathrm{x}\right)=\left(\lambda−\int\:\mathrm{x}^{\mathrm{3}} \:\mathrm{e}^{−\mathrm{cosx}} \mathrm{dx}\right)\mathrm{e}^{\mathrm{cosx}} \\ $$
