
Question Number 133905 by mohammad17 last updated on 25/Feb/21

Answered by Dwaipayan Shikari last updated on 25/Feb/21
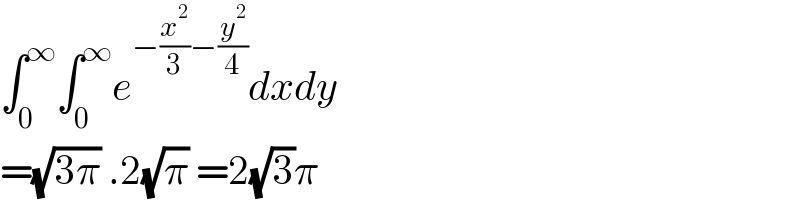
$$\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{{y}^{\mathrm{2}} }{\mathrm{4}}} {dxdy} \\ $$$$=\sqrt{\mathrm{3}\pi}\:.\mathrm{2}\sqrt{\pi}\:=\mathrm{2}\sqrt{\mathrm{3}}\pi \\ $$
Answered by mathmax by abdo last updated on 25/Feb/21
![I=∫∫_R^+^2 e^(−(x^2 /3)−(y^2 /4)) dxdy with diffeomorphism { ((x=(√3)rcosθ)),((y=2rsinθ we get)) :} I =∫_0 ^∞ ∫_0 ^(π/2) e^(−r^2 ) (2(√3))r drdθ =(π/2)(2(√3)) ∫_0 ^∞ r e^(−r^2 ) dr =π(√3)[−(1/2)e^(−r^2 ) ]_0 ^∞ =((π(√3))/2)](Q133959.png)
$$\mathrm{I}=\int\int_{\mathrm{R}^{+^{\mathrm{2}} } } \:\:\:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{4}}} \:\mathrm{dxdy}\:\mathrm{with}\:\mathrm{diffeomorphism}\:\:\begin{cases}{\mathrm{x}=\sqrt{\mathrm{3}}\mathrm{rcos}\theta}\\{\mathrm{y}=\mathrm{2rsin}\theta\:\:\:\mathrm{we}\:\mathrm{get}}\end{cases} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \left(\mathrm{2}\sqrt{\mathrm{3}}\right)\mathrm{r}\:\mathrm{drd}\theta \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{r}\:\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \mathrm{dr}\:=\pi\sqrt{\mathrm{3}}\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} \:=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$ \\ $$
