
Question Number 133840 by Algoritm last updated on 24/Feb/21
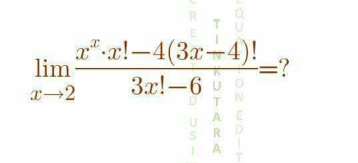
Answered by Dwaipayan Shikari last updated on 24/Feb/21
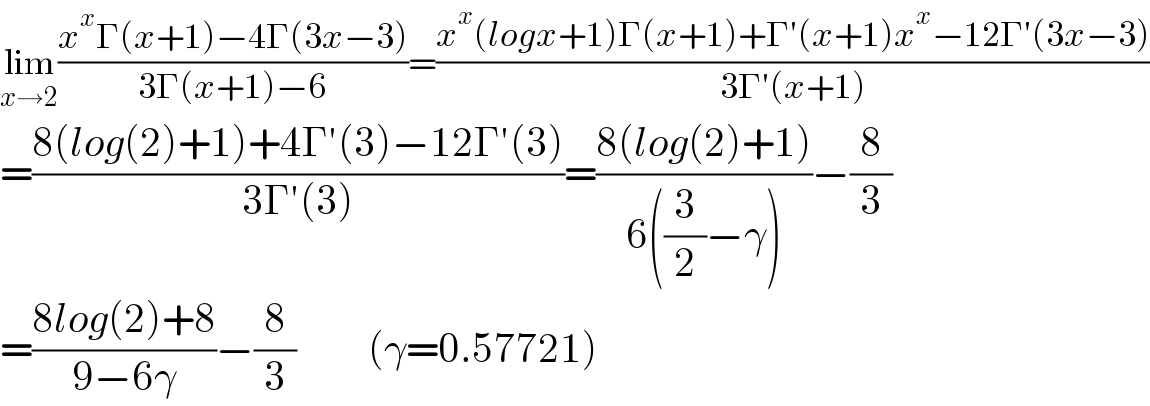
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{x}^{{x}} \Gamma\left({x}+\mathrm{1}\right)−\mathrm{4}\Gamma\left(\mathrm{3}{x}−\mathrm{3}\right)}{\mathrm{3}\Gamma\left({x}+\mathrm{1}\right)−\mathrm{6}}=\frac{{x}^{{x}} \left({logx}+\mathrm{1}\right)\Gamma\left({x}+\mathrm{1}\right)+\Gamma'\left({x}+\mathrm{1}\right){x}^{{x}} −\mathrm{12}\Gamma'\left(\mathrm{3}{x}−\mathrm{3}\right)}{\mathrm{3}\Gamma'\left({x}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{8}\left({log}\left(\mathrm{2}\right)+\mathrm{1}\right)+\mathrm{4}\Gamma'\left(\mathrm{3}\right)−\mathrm{12}\Gamma'\left(\mathrm{3}\right)}{\mathrm{3}\Gamma'\left(\mathrm{3}\right)}=\frac{\mathrm{8}\left({log}\left(\mathrm{2}\right)+\mathrm{1}\right)}{\mathrm{6}\left(\frac{\mathrm{3}}{\mathrm{2}}−\gamma\right)}−\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{8}{log}\left(\mathrm{2}\right)+\mathrm{8}}{\mathrm{9}−\mathrm{6}\gamma}−\frac{\mathrm{8}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\left(\gamma=\mathrm{0}.\mathrm{57721}\right) \\ $$
Commented by SLVR last updated on 13/Apr/21
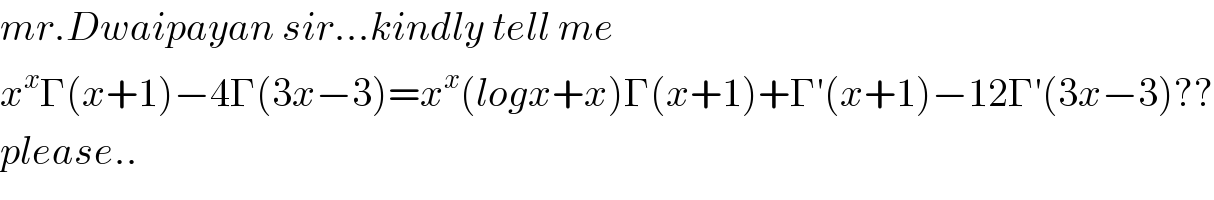
$${mr}.{Dwaipayan}\:{sir}...{kindly}\:{tell}\:{me} \\ $$$${x}^{{x}} \Gamma\left({x}+\mathrm{1}\right)−\mathrm{4}\Gamma\left(\mathrm{3}{x}−\mathrm{3}\right)={x}^{{x}} \left({logx}+{x}\right)\Gamma\left({x}+\mathrm{1}\right)+\Gamma'\left({x}+\mathrm{1}\right)−\mathrm{12}\Gamma'\left(\mathrm{3}{x}−\mathrm{3}\right)?? \\ $$$${please}.. \\ $$
