
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 133658 by liberty last updated on 23/Feb/21

Commented by mr W last updated on 23/Feb/21

$${i}\:{get}\:{headache}\:{when}\:{reading}\:{such} \\ $$$${colorful}\:{text},\:{not}\:{to}\:{mention}\:{to}\:{find} \\ $$$$\left.{the}\:{correct}\:{solution}\::\right) \\ $$
Commented by liberty last updated on 23/Feb/21
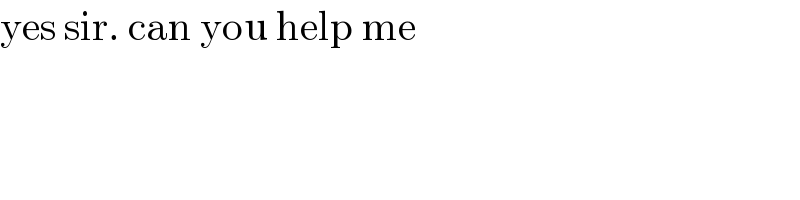
$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{can}\:\mathrm{you}\:\mathrm{help}\:\mathrm{me} \\ $$
Commented by EDWIN88 last updated on 23/Feb/21
A math competition attended by 2019 participants. For every two participants in the competition both know or don't know each other. It is known that none of the three participants in the race knew each other. Suppose m is a natural number so that: each participant knows at most m of the other participants. For each natural number k with 1 <k <m, there should be at least one participant who knows the other k participants. The largest possible m-value is ... (a) 1250 (b) 1300 (c) 1346 (d) 1388 (e) 1450
