
Question Number 133199 by rexford last updated on 19/Feb/21
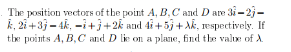
Answered by mr W last updated on 20/Feb/21

$$\overset{\rightarrow} {\boldsymbol{{AB}}}=\left(−\mathrm{1},\mathrm{5},−\mathrm{3}\right) \\ $$$$\overset{\rightarrow} {\boldsymbol{{AC}}}=\left(−\mathrm{4},\mathrm{3},\mathrm{3}\right) \\ $$$$\overset{\rightarrow} {\boldsymbol{{AD}}}=\left(\mathrm{1},\mathrm{7},\lambda+\mathrm{1}\right) \\ $$$$\mathrm{1}×\left(\mathrm{15}+\mathrm{9}\right)−\mathrm{7}×\left(−\mathrm{3}−\mathrm{12}\right)+\left(\lambda+\mathrm{1}\right)\left(−\mathrm{3}+\mathrm{20}\right)=\mathrm{0} \\ $$$$\mathrm{24}+\mathrm{7}×\mathrm{15}+\mathrm{17}\left(\lambda+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda=−\frac{\mathrm{146}}{\mathrm{17}} \\ $$
Commented by liberty last updated on 20/Feb/21
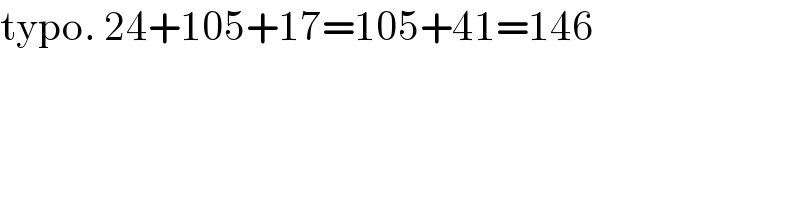
$$\mathrm{typo}.\:\mathrm{24}+\mathrm{105}+\mathrm{17}=\mathrm{105}+\mathrm{41}=\mathrm{146} \\ $$
Commented by mr W last updated on 20/Feb/21

$${yes},\:{thanks}! \\ $$
Commented by rexford last updated on 20/Feb/21

$${Thanks} \\ $$
Answered by john_santu last updated on 20/Feb/21

$$\mathrm{let}\:\overset{\rightarrow} {\mathrm{n}}\:=\:\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}\:\mathrm{be}\:\mathrm{a}\:\mathrm{normal}\:\mathrm{vector}\:\mathrm{plane} \\ $$$$\mathrm{then}\:\overset{\rightarrow} {\mathrm{n}}\:=\:\begin{vmatrix}{\mathrm{3}\:\:\:\:−\mathrm{2}\:\:\:\:\:−\mathrm{1}}\\{\mathrm{2}\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:−\mathrm{4}}\end{vmatrix}=\:\mathrm{11}\hat {\mathrm{i}}+\mathrm{10}\hat {\mathrm{j}}+\mathrm{13}\hat {\mathrm{k}} \\ $$$$\mathrm{since}\:\mathrm{the}\:\mathrm{points}\:\mathrm{A},\mathrm{B},\mathrm{C}\:\mathrm{and}\:\mathrm{D}\: \\ $$$$\mathrm{so}\:\overset{\rightarrow} {\mathrm{n}}.\boldsymbol{\mathrm{CD}}\:=\:\mathrm{0}\:;\:\mathrm{where}\:\boldsymbol{\mathrm{CD}}\:=\:\left(\mathrm{5},\mathrm{4},\lambda−\mathrm{2}\right) \\ $$$$\Leftrightarrow\:\mathrm{55}+\mathrm{40}+\mathrm{13}\lambda−\mathrm{26}=\mathrm{0} \\ $$$$\Leftrightarrow\:\lambda\:=\:\frac{\mathrm{26}}{\mathrm{99}}\: \\ $$
Answered by EDWIN88 last updated on 20/Feb/21
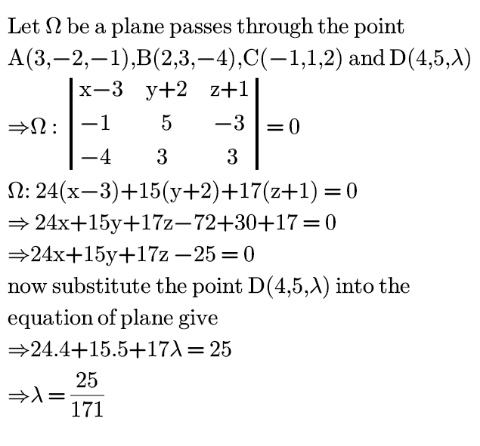
Answered by liberty last updated on 20/Feb/21

$$\mathrm{normal}\:\mathrm{vector}\:\mathrm{plane}\: \\ $$$$\overset{\rightarrow} {\mathrm{n}}\:=\mathrm{AB}×\mathrm{AC}\:=\begin{vmatrix}{−\mathrm{1}\:\:\:\:\:\:\:\mathrm{5}\:\:\:\:\:\:−\mathrm{3}\:\:\:\:}\\{−\mathrm{4}\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\mathrm{3}}\end{vmatrix} \\ $$$$\overset{\rightarrow} {\mathrm{n}}=\:\mathrm{24}\hat {\mathrm{i}}+\mathrm{15}\hat {\mathrm{j}}+\mathrm{17}\hat {\mathrm{k}} \\ $$$$\mathrm{put}\:\mathrm{AD}\:=\:\hat {\mathrm{i}}+\mathrm{7}\hat {\mathrm{j}}+\left(\lambda+\mathrm{1}\right)\hat {\mathrm{k}} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{get}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{plane}\:\mathrm{is} \\ $$$$\overset{\rightarrow} {\mathrm{n}}.\mathrm{AD}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{24}+\mathrm{105}+\mathrm{17}\lambda+\mathrm{17}\:=\:\mathrm{0} \\ $$$$\Rightarrow\lambda=−\frac{\mathrm{146}}{\mathrm{17}} \\ $$
Commented by rexford last updated on 20/Feb/21
$${Thank}\:{you}\:{very}\:{much} \\ $$
