
Question Number 133194 by Algoritm last updated on 19/Feb/21
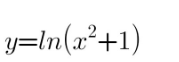
Commented by Algoritm last updated on 19/Feb/21

$$\frac{\mathrm{d}^{\mathrm{n}} \mathrm{y}}{\mathrm{dx}^{\mathrm{n}} }=? \\ $$
Commented by mr W last updated on 20/Feb/21

$${very}\:{strange}! \\ $$$${does}\:{this}\:{guy}\:{really}\:{have}\:{many} \\ $$$${suporters}\:{or}\:{he}\:{just}\:{uses}\:{many} \\ $$$${different}\:{IDs}?\:{each}\:{time}\:{when}\:{he} \\ $$$${has}\:{posted}\:{a}\:{question},\:{no}\:{matter}\:{how} \\ $$$${good}\:{or}\:{bad}\:{the}\:{question}\:{is},\:{the}\:{post} \\ $$$${is}\:\boldsymbol{{immediately}}\:{liked}\:{one}\:{or}\:{more} \\ $$$${times}.\:{i}\:{can}'{t}\:{beleave}\:{that}\:{these}\:{likes} \\ $$$${are}\:{seriously}\:{meant}\:{and}\:{don}'{t} \\ $$$${understand}\:{what}\:{they}\:{are}\:{good}\:{for}. \\ $$
Answered by Olaf last updated on 19/Feb/21
![f(x) = ln(x^2 +1) = ln(x−i)+ln(x+i) f′(x) = ((2x)/(1+x^2 )) = (1/(x−i))+(1/(x+i)) f^((n)) = (((−1)^(n−1) (n−1)!)/((x−i)^n ))+(((−1)^(n−1) (n−1)!)/((x+i)^n )) f^((n)) = (−1)^(n−1) (n−1)![(1/((x−i)^n ))+(1/((x+i)^n ))] f^((n)) = (−1)^n (n−1)![(((x+i)^n +(x−i)^n )/((x^2 +1)^n ))] f^((n)) = (−1)^(n−1) (n−1)![((Σ_(k=0) ^n C_k ^n x^k i^(n−k) +Σ_(k=0) ^n C_k ^n x^k (−i)^(n−k) )/((x^2 +1)^n ))] f^((n)) = (−1)^(n−1) (n−1)![((Σ_(k=0) ^n C_k ^n x^(n−k) (i^k +(−i)^k ))/((x^2 +1)^n ))] f^((n)) = (−1)^(n−1) (n−1)![((Σ_(p=0) ^(⌊(n/2)⌋) C_(2p) ^n x^(n−2p) i^(2p) (1+(−1)^(2p) ))/((x^2 +1)^n ))] f^((n)) = (−1)^(n−1) (n−1)![((Σ_(p=0) ^(⌊(n/2)⌋) C_(2p) ^n x^(n−2p) (−1)^p ×2)/((x^2 +1)^n ))] f^((n)) = 2(−1)^(n−1) (n−1)![((Σ_(p=0) ^(⌊(n/2)⌋) (−1)^p C_(2p) ^n x^(n−2p) )/((x^2 +1)^n ))]](Q133196.png)
$${f}\left({x}\right)\:=\:\mathrm{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\:=\:\mathrm{ln}\left({x}−{i}\right)+\mathrm{ln}\left({x}+{i}\right) \\ $$$${f}'\left({x}\right)\:=\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{{x}−{i}}+\frac{\mathrm{1}}{{x}+{i}} \\ $$$${f}^{\left({n}\right)} \:=\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}−{i}\right)^{{n}} }+\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({x}+{i}\right)^{{n}} } \\ $$$${f}^{\left({n}\right)} \:=\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left[\frac{\mathrm{1}}{\left({x}−{i}\right)^{{n}} }+\frac{\mathrm{1}}{\left({x}+{i}\right)^{{n}} }\right] \\ $$$${f}^{\left({n}\right)} \:=\:\left(−\mathrm{1}\right)^{{n}} \left({n}−\mathrm{1}\right)!\left[\frac{\left({x}+{i}\right)^{{n}} +\left({x}−{i}\right)^{{n}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{n}} }\right] \\ $$$${f}^{\left({n}\right)} \:=\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left[\frac{\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{C}_{{k}} ^{{n}} {x}^{{k}} {i}^{{n}−{k}} +\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{C}_{{k}} ^{{n}} {x}^{{k}} \left(−{i}\right)^{{n}−{k}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{n}} }\right] \\ $$$${f}^{\left({n}\right)} \:=\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left[\frac{\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{C}_{{k}} ^{{n}} {x}^{{n}−{k}} \left({i}^{{k}} +\left(−{i}\right)^{{k}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{n}} }\right] \\ $$$${f}^{\left({n}\right)} \:=\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left[\frac{\underset{{p}=\mathrm{0}} {\overset{\lfloor\frac{{n}}{\mathrm{2}}\rfloor} {\sum}}\mathrm{C}_{\mathrm{2}{p}} ^{{n}} {x}^{{n}−\mathrm{2}{p}} {i}^{\mathrm{2}{p}} \left(\mathrm{1}+\left(−\mathrm{1}\right)^{\mathrm{2}{p}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{n}} }\right] \\ $$$${f}^{\left({n}\right)} \:=\:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left[\frac{\underset{{p}=\mathrm{0}} {\overset{\lfloor\frac{{n}}{\mathrm{2}}\rfloor} {\sum}}\mathrm{C}_{\mathrm{2}{p}} ^{{n}} {x}^{{n}−\mathrm{2}{p}} \left(−\mathrm{1}\right)^{{p}} ×\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{n}} }\right] \\ $$$${f}^{\left({n}\right)} \:=\:\mathrm{2}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!\left[\frac{\underset{{p}=\mathrm{0}} {\overset{\lfloor\frac{{n}}{\mathrm{2}}\rfloor} {\sum}}\left(−\mathrm{1}\right)^{{p}} \mathrm{C}_{\mathrm{2}{p}} ^{{n}} {x}^{{n}−\mathrm{2}{p}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{n}} }\right] \\ $$
