Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 133180 by mathlove last updated on 19/Feb/21

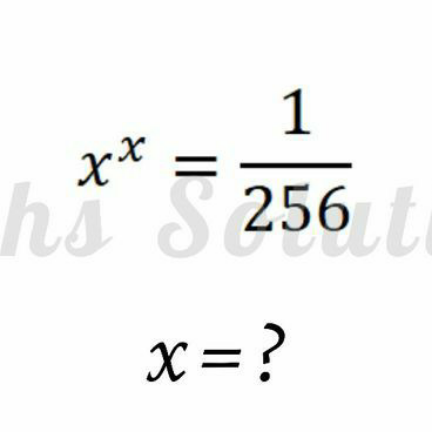
Commented by mr W last updated on 19/Feb/21

no real solution! x^x ≥(1/( (e)^(1/e) ))≈0.692 (1/(256))<<0.692 ⇒x^x =(1/(256)) is not possible!

$${no}\:{real}\:{solution}! \\ $$$${x}^{{x}} \geqslant\frac{\mathrm{1}}{\:\sqrt[{{e}}]{{e}}}\approx\mathrm{0}.\mathrm{692} \\ $$$$\frac{\mathrm{1}}{\mathrm{256}}<<\mathrm{0}.\mathrm{692} \\ $$$$\Rightarrow{x}^{{x}} =\frac{\mathrm{1}}{\mathrm{256}}\:{is}\:{not}\:{possible}! \\ $$

Commented by mr W last updated on 20/Feb/21

generally the equation x^x =a has • no solution if a<(1/( (e)^(1/e) ))≈0.692 • one solution if a=(1/( (e)^(1/e) )) • two solutions if (1/( (e)^(1/e) ))<a<1 • one solution if a≥1 the solution(s) is (are): x=e^(W(ln a))

$${generally} \\ $$$${the}\:{equation}\:{x}^{{x}} ={a}\:{has} \\ $$$$\bullet\:{no}\:{solution}\:{if}\:{a}<\frac{\mathrm{1}}{\:\sqrt[{{e}}]{{e}}}\approx\mathrm{0}.\mathrm{692} \\ $$$$\bullet\:{one}\:{solution}\:{if}\:{a}=\frac{\mathrm{1}}{\:\sqrt[{{e}}]{{e}}} \\ $$$$\bullet\:{two}\:{solutions}\:{if}\:\frac{\mathrm{1}}{\:\sqrt[{{e}}]{{e}}}<{a}<\mathrm{1} \\ $$$$\bullet\:{one}\:{solution}\:{if}\:{a}\geqslant\mathrm{1} \\ $$$$ \\ $$$${the}\:{solution}\left({s}\right)\:{is}\:\left({are}\right): \\ $$$${x}={e}^{\mathbb{W}\left(\mathrm{ln}\:{a}\right)} \\ $$

Commented by Tawa11 last updated on 23/Jul/21

great

$$\mathrm{great} \\ $$

Answered by JDamian last updated on 19/Feb/21

x = −4

$${x}\:=\:−\mathrm{4} \\ $$

Commented by liberty last updated on 20/Feb/21

Commented by mr W last updated on 20/Feb/21

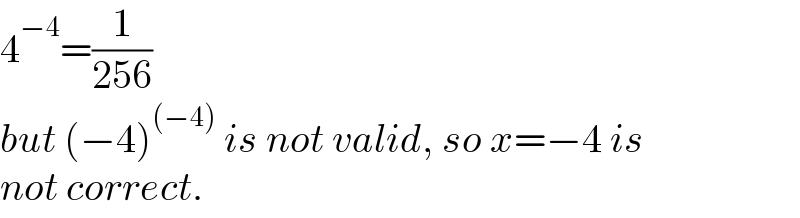
4^(−4) =(1/(256)) but (−4)^((−4)) is not valid, so x=−4 is not correct.

$$\mathrm{4}^{−\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{256}} \\ $$$${but}\:\left(−\mathrm{4}\right)^{\left(−\mathrm{4}\right)} \:{is}\:{not}\:{valid},\:{so}\:{x}=−\mathrm{4}\:{is} \\ $$$${not}\:{correct}. \\ $$

Commented by liberty last updated on 20/Feb/21

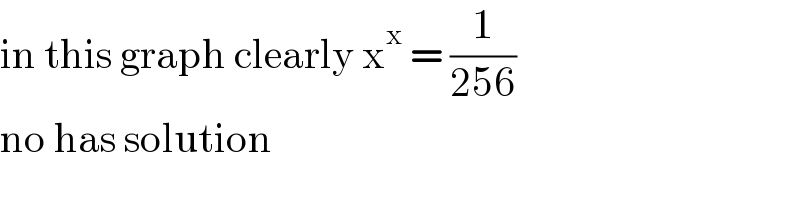
in this graph clearly x^x = (1/(256)) no has solution

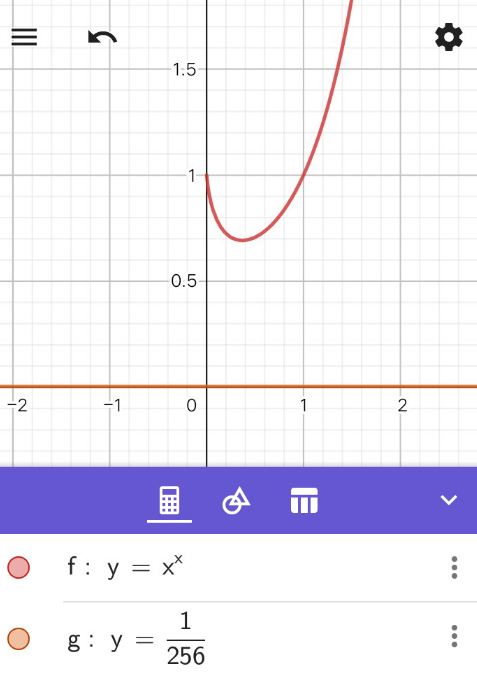
$$\mathrm{in}\:\mathrm{this}\:\mathrm{graph}\:\mathrm{clearly}\:\mathrm{x}^{\mathrm{x}} \:=\:\frac{\mathrm{1}}{\mathrm{256}} \\ $$$$\mathrm{no}\:\mathrm{has}\:\mathrm{solution} \\ $$

Commented by JDamian last updated on 20/Feb/21

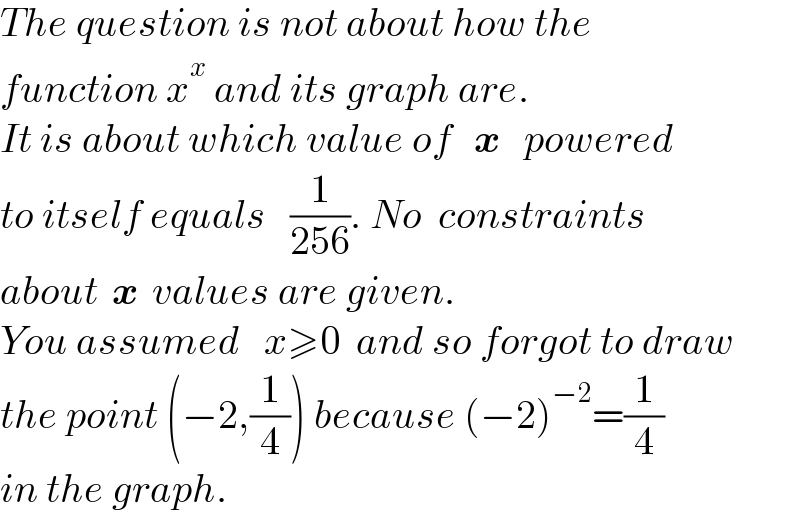
The question is not about how the function x^x and its graph are. It is about which value of x powered to itself equals (1/(256)). No constraints about x values are given. You assumed x≥0 and so forgot to draw the point (−2,(1/4)) because (−2)^(−2) =(1/4) in the graph.

$${The}\:{question}\:{is}\:{not}\:{about}\:{how}\:{the} \\ $$$${function}\:{x}^{{x}} \:{and}\:{its}\:{graph}\:{are}. \\ $$$${It}\:{is}\:{about}\:{which}\:{value}\:{of}\:\:\:\boldsymbol{{x}}\:\:\:{powered} \\ $$$${to}\:{itself}\:{equals}\:\:\:\frac{\mathrm{1}}{\mathrm{256}}.\:{No}\:\:{constraints} \\ $$$${about}\:\:\boldsymbol{{x}}\:\:{values}\:{are}\:{given}. \\ $$$${You}\:{assumed}\:\:\:{x}\geqslant\mathrm{0}\:\:{and}\:{so}\:{forgot}\:{to}\:{draw} \\ $$$${the}\:{point}\:\left(−\mathrm{2},\frac{\mathrm{1}}{\mathrm{4}}\right)\:{because}\:\left(−\mathrm{2}\right)^{−\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${in}\:{the}\:{graph}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com