
Question Number 132869 by syamilkamil1 last updated on 17/Feb/21
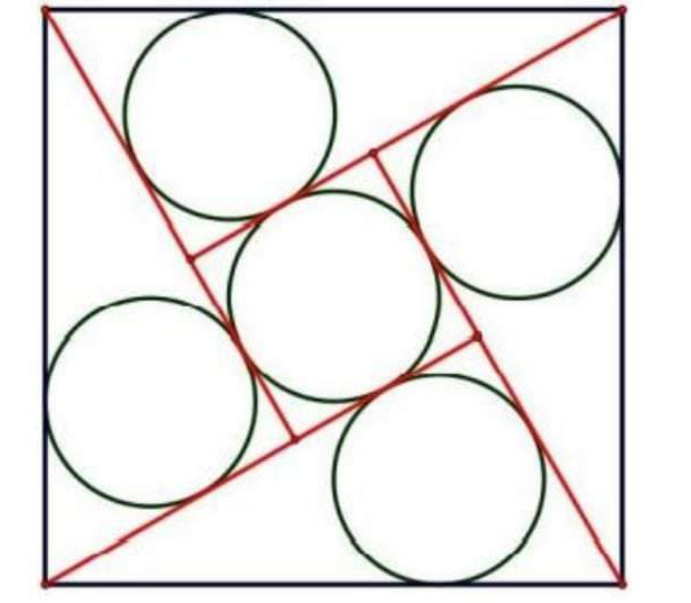
Commented by syamilkamil1 last updated on 17/Feb/21
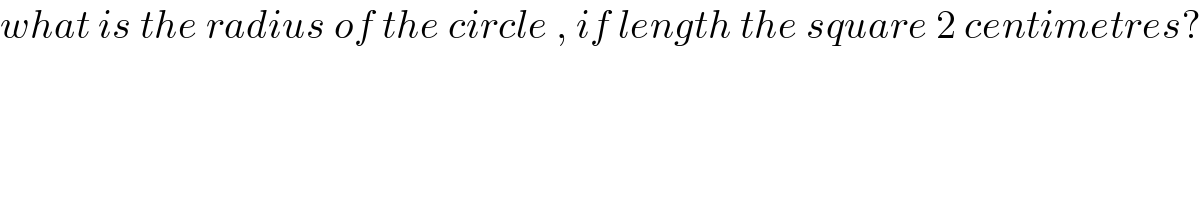
$${what}\:{is}\:{the}\:{radius}\:{of}\:{the}\:{circle}\:,\:{if}\:{length}\:{the}\:{square}\:\mathrm{2}\:{centimetres}? \\ $$
Commented by bramlexs22 last updated on 17/Feb/21

$$\mathrm{r}\:=\:\frac{\mathrm{1}}{\mathrm{4}}{a}\:\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\: \\ $$
Answered by mr W last updated on 17/Feb/21
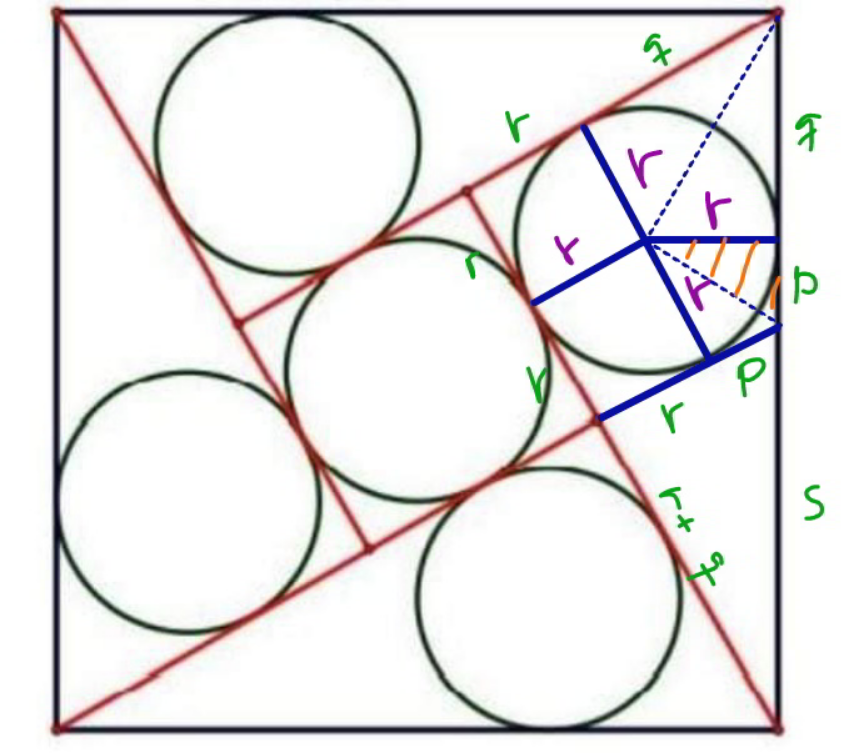
Commented by mr W last updated on 17/Feb/21

$$\frac{{p}}{{r}}=\frac{{r}}{{q}} \\ $$$$\Rightarrow{q}=\frac{{r}^{\mathrm{2}} }{{p}} \\ $$$$\frac{{r}+{p}}{{r}+{q}}=\frac{{r}+{q}}{\mathrm{3}{r}+{q}} \\ $$$$\frac{{r}+{p}}{{r}+\frac{{r}^{\mathrm{2}} }{{p}}}=\frac{{r}+\frac{{r}^{\mathrm{2}} }{{p}}}{\mathrm{3}{r}+\frac{{r}^{\mathrm{2}} }{{p}}} \\ $$$$\mathrm{3}{p}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow{p}=\frac{{r}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{q}=\sqrt{\mathrm{3}}{r} \\ $$$${s}=\sqrt{\left({r}+{p}\right)^{\mathrm{2}} +\left({r}+{q}\right)^{\mathrm{2}} } \\ $$$$={r}\sqrt{\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}\sqrt{\mathrm{6}\left(\sqrt{\mathrm{3}}+\mathrm{2}\right)}}{\mathrm{3}}{r} \\ $$$${a}={p}+{q}+{s}=\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\sqrt{\mathrm{3}}+\frac{\mathrm{2}\sqrt{\mathrm{6}\left(\sqrt{\mathrm{3}}+\mathrm{2}\right)}}{\mathrm{3}}\right){r} \\ $$$${a}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{2}+\sqrt{\mathrm{2}\left(\sqrt{\mathrm{3}}+\mathrm{2}\right)}\right){r}=\mathrm{2}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right){r} \\ $$$$\Rightarrow{r}=\frac{{a}}{\mathrm{2}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)}=\frac{\left(\sqrt{\mathrm{3}}−\mathrm{1}\right){a}}{\mathrm{4}} \\ $$
