Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 132293 by Algoritm last updated on 13/Feb/21

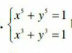
Commented by mr W last updated on 13/Feb/21

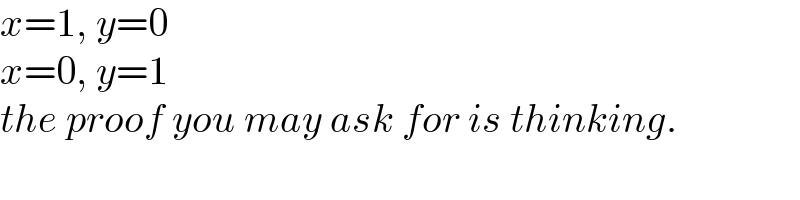
x=1, y=0 x=0, y=1 the proof you may ask for is thinking.

$${x}=\mathrm{1},\:{y}=\mathrm{0} \\ $$$${x}=\mathrm{0},\:{y}=\mathrm{1} \\ $$$${the}\:{proof}\:{you}\:{may}\:{ask}\:{for}\:{is}\:{thinking}. \\ $$

Answered by MJS_new last updated on 13/Feb/21

{ ((x^5 +y^5 =1)),((x^3 +y^3 =1)) :} let x=u−v∧y=u+v { ((2u^5 +20u^3 v^2 +10uv^4 −1=0)),((2u^3 +6uv^2 −1=0 ⇒ v^2 =((1−2u^3 )/(6u)))) :} insert in (1) and transform ⇒ u^6 −(5/8)u^3 +(9/(32))u−(5/(64))=0 (u−(1/2))^3 (u^3 +(3/2)u^2 +(3/2)u+(5/8))=0 now use Cardano ⇒ u_(1, 2, 3) =(1/2) u_4 =−(1/2)+α−β u_5 =−(1/2)+ωα−ω^2 β u_6 =−(1/2)+ω^2 α−ωβ with α=(((−1+(√5))/(16)))^(1/3) ∧β=(((1+(√5))/(16)))^(1/3) ∧ω=−(1/2)+((√3)/2)i ⇒ 6 solutions x=0∧y=1 ∨ x=1∧y=0 x≈−.661093±.630705i∧y=x^− x≈−.791887±.755487∧y=−.0470208±.998894i

$$\begin{cases}{{x}^{\mathrm{5}} +{y}^{\mathrm{5}} =\mathrm{1}}\\{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\mathrm{1}}\end{cases} \\ $$$$\mathrm{let}\:{x}={u}−{v}\wedge{y}={u}+{v} \\ $$$$\begin{cases}{\mathrm{2}{u}^{\mathrm{5}} +\mathrm{20}{u}^{\mathrm{3}} {v}^{\mathrm{2}} +\mathrm{10}{uv}^{\mathrm{4}} −\mathrm{1}=\mathrm{0}}\\{\mathrm{2}{u}^{\mathrm{3}} +\mathrm{6}{uv}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\Rightarrow\:{v}^{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{2}{u}^{\mathrm{3}} }{\mathrm{6}{u}}}\end{cases} \\ $$$$\mathrm{insert}\:\mathrm{in}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\mathrm{transform}\:\Rightarrow \\ $$$${u}^{\mathrm{6}} −\frac{\mathrm{5}}{\mathrm{8}}{u}^{\mathrm{3}} +\frac{\mathrm{9}}{\mathrm{32}}{u}−\frac{\mathrm{5}}{\mathrm{64}}=\mathrm{0} \\ $$$$\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} \left({u}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}}{u}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}{u}+\frac{\mathrm{5}}{\mathrm{8}}\right)=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{Cardano} \\ $$$$\Rightarrow \\ $$$${u}_{\mathrm{1},\:\mathrm{2},\:\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${u}_{\mathrm{4}} =−\frac{\mathrm{1}}{\mathrm{2}}+\alpha−\beta \\ $$$${u}_{\mathrm{5}} =−\frac{\mathrm{1}}{\mathrm{2}}+\omega\alpha−\omega^{\mathrm{2}} \beta \\ $$$${u}_{\mathrm{6}} =−\frac{\mathrm{1}}{\mathrm{2}}+\omega^{\mathrm{2}} \alpha−\omega\beta \\ $$$$\mathrm{with}\:\alpha=\sqrt[{\mathrm{3}}]{\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{16}}}\wedge\beta=\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{16}}}\wedge\omega=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$\Rightarrow \\ $$$$\mathrm{6}\:\mathrm{solutions} \\ $$$${x}=\mathrm{0}\wedge{y}=\mathrm{1}\:\vee\:{x}=\mathrm{1}\wedge{y}=\mathrm{0} \\ $$$${x}\approx−.\mathrm{661093}\pm.\mathrm{630705i}\wedge{y}=\overset{−} {{x}} \\ $$$${x}\approx−.\mathrm{791887}\pm.\mathrm{755487}\wedge{y}=−.\mathrm{0470208}\pm.\mathrm{998894i} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com