
Question Number 132098 by rs4089 last updated on 11/Feb/21

Answered by Ar Brandon last updated on 11/Feb/21
![S_n =Σ_(k=1) ^n (n/(n^2 +kn+k^2 )) lim_(n→∞) S_n =lim_(n→∞) (1/n)Σ_(k=1) ^n (1/(1+(k/n)+(k^2 /n^2 ))) =∫_0 ^1 (dx/(x^2 +x+1))=∫_0 ^1 (dx/((x+(1/2))^2 +(3/4)))=(2/( (√3)))[tan^(−1) (((2x+1)/( (√3))))]_0 ^1 =(2/( (√3)))((π/3)−(π/6))=(π/(3(√3)))](Q132101.png)
$$\mathrm{S}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{n}}{\mathrm{n}^{\mathrm{2}} +\mathrm{kn}+\mathrm{k}^{\mathrm{2}} } \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}S}_{\mathrm{n}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}+\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{6}}\right)=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Commented by Ar Brandon last updated on 11/Feb/21
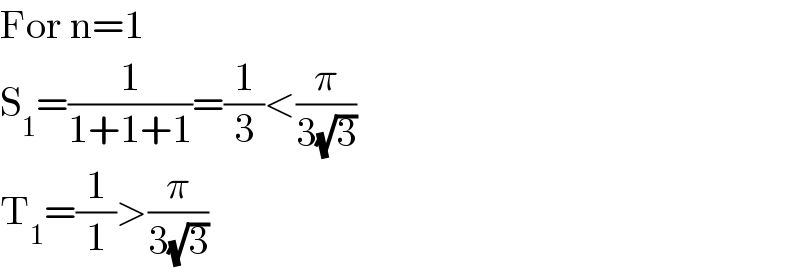
$$\mathrm{For}\:\mathrm{n}=\mathrm{1} \\ $$$$\mathrm{S}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}<\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{T}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}}>\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
