
Question Number 131745 by liberty last updated on 08/Feb/21

Commented by guyyy last updated on 18/Feb/21

Commented by guyyy last updated on 18/Feb/21

Commented by guyyy last updated on 18/Feb/21

Commented by guyyy last updated on 18/Feb/21

Answered by bemath last updated on 08/Feb/21
![(2) lim_(n→∞) [(1+(1/n^2 ))^n^2 ]^((4(sin (π/(2n))))/(π/(2n))) = e^(lim_(n→∞) (((4sin (π/(2n)))/(π/(2n))))) = e^4](Q131747.png)
$$\left(\mathrm{2}\right)\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)^{\mathrm{n}^{\mathrm{2}} } \right]^{\frac{\mathrm{4}\left(\mathrm{sin}\:\frac{\pi}{\mathrm{2n}}\right)}{\frac{\pi}{\mathrm{2n}}}} =\:\mathrm{e}^{\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{4sin}\:\frac{\pi}{\mathrm{2n}}}{\frac{\pi}{\mathrm{2n}}}\right)} \:=\:\mathrm{e}^{\mathrm{4}} \\ $$
Answered by bemath last updated on 08/Feb/21
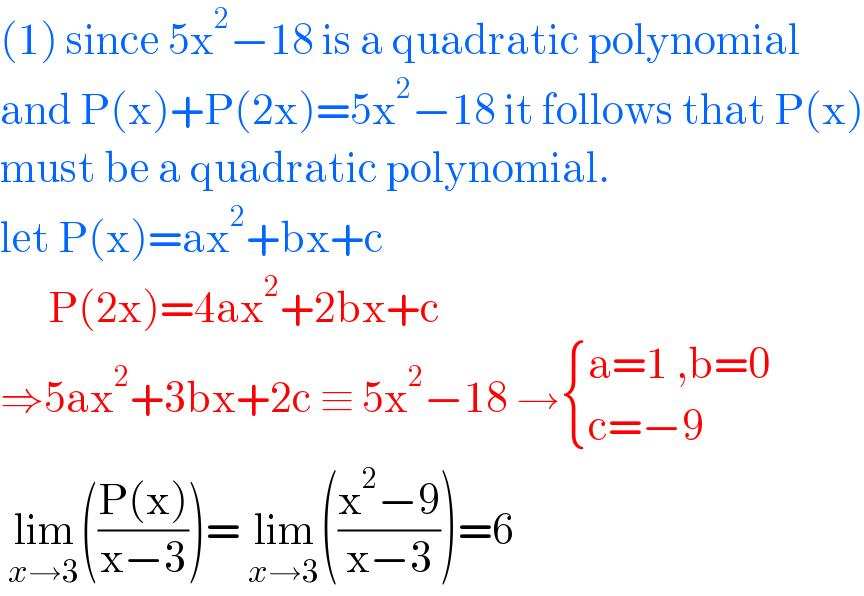
$$\left(\mathrm{1}\right)\:\mathrm{since}\:\mathrm{5x}^{\mathrm{2}} −\mathrm{18}\:\mathrm{is}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{polynomial} \\ $$$$\mathrm{and}\:\mathrm{P}\left(\mathrm{x}\right)+\mathrm{P}\left(\mathrm{2x}\right)=\mathrm{5x}^{\mathrm{2}} −\mathrm{18}\:\mathrm{it}\:\mathrm{follows}\:\mathrm{that}\:\mathrm{P}\left(\mathrm{x}\right) \\ $$$$\mathrm{must}\:\mathrm{be}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{polynomial}.\: \\ $$$$\mathrm{let}\:\mathrm{P}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}\: \\ $$$$\:\:\:\:\:\:\mathrm{P}\left(\mathrm{2x}\right)=\mathrm{4ax}^{\mathrm{2}} +\mathrm{2bx}+\mathrm{c}\: \\ $$$$\Rightarrow\mathrm{5ax}^{\mathrm{2}} +\mathrm{3bx}+\mathrm{2c}\:\equiv\:\mathrm{5x}^{\mathrm{2}} −\mathrm{18}\:\rightarrow\begin{cases}{\mathrm{a}=\mathrm{1}\:,\mathrm{b}=\mathrm{0}}\\{\mathrm{c}=−\mathrm{9}}\end{cases} \\ $$$$\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\left(\frac{\mathrm{P}\left(\mathrm{x}\right)}{\mathrm{x}−\mathrm{3}}\right)=\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\left(\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{9}}{\mathrm{x}−\mathrm{3}}\right)=\mathrm{6} \\ $$
Answered by bemath last updated on 08/Feb/21
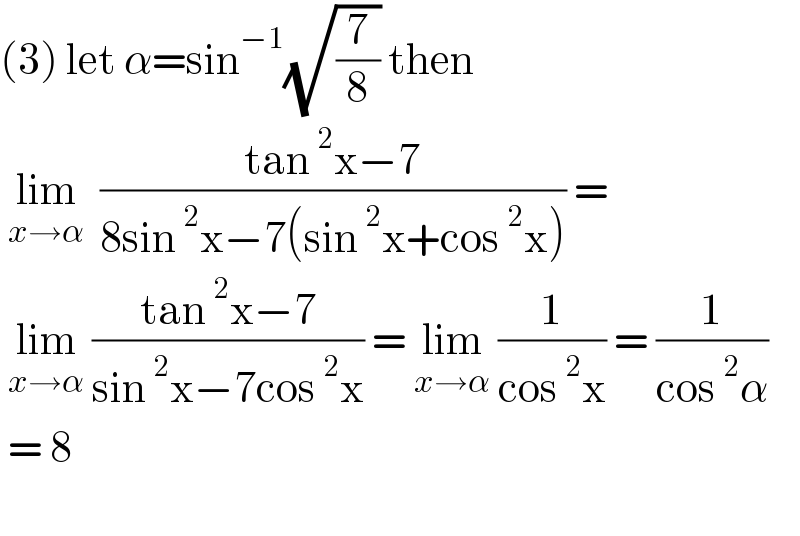
$$\left(\mathrm{3}\right)\:\mathrm{let}\:\alpha=\mathrm{sin}^{−\mathrm{1}} \sqrt{\frac{\mathrm{7}}{\mathrm{8}}}\:\mathrm{then}\: \\ $$$$\:\underset{{x}\rightarrow\alpha} {\mathrm{lim}}\:\:\frac{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{7}}{\mathrm{8sin}\:^{\mathrm{2}} \mathrm{x}−\mathrm{7}\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\right)}\:=\: \\ $$$$\:\underset{{x}\rightarrow\alpha} {\mathrm{lim}}\:\frac{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{7}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}−\mathrm{7cos}\:^{\mathrm{2}} \mathrm{x}}\:=\:\underset{{x}\rightarrow\alpha} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:=\:\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \alpha} \\ $$$$\:=\:\mathrm{8}\: \\ $$$$ \\ $$
Commented by guyyy last updated on 13/Feb/21

