
Question Number 131665 by naka3546 last updated on 07/Feb/21
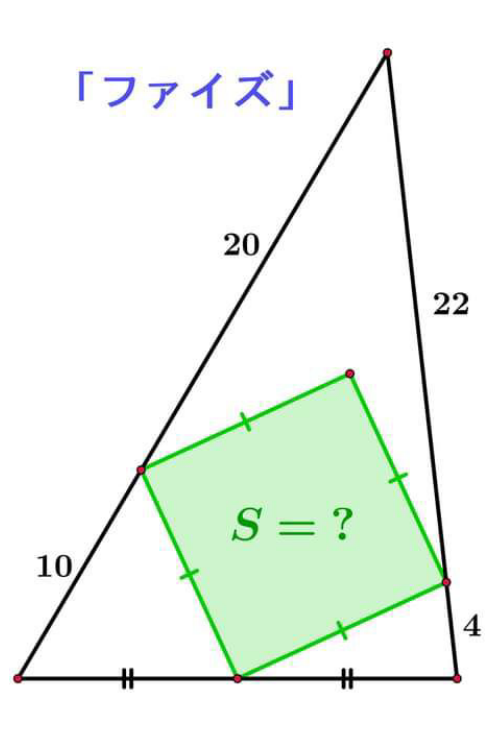
Answered by mr W last updated on 07/Feb/21
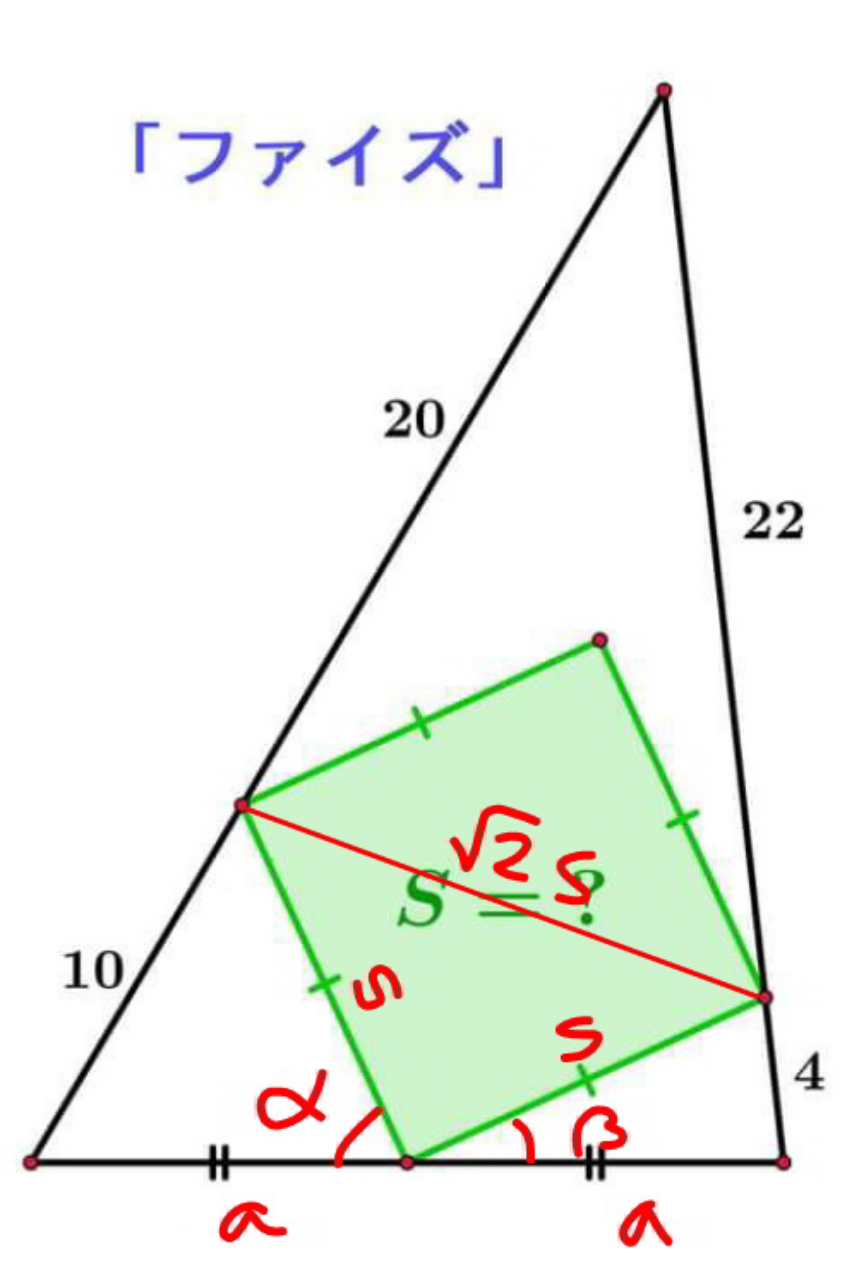
Commented by mr W last updated on 07/Feb/21

$$\frac{\mathrm{20}^{\mathrm{2}} +\mathrm{22}^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}{s}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{20}×\mathrm{22}}=\frac{\mathrm{30}^{\mathrm{2}} +\mathrm{26}^{\mathrm{2}} −\left(\mathrm{2}{a}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{30}×\mathrm{26}} \\ $$$$\Rightarrow\frac{\mathrm{442}−{s}^{\mathrm{2}} }{\mathrm{22}}=\frac{\mathrm{788}−\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{39}}\:\:\:...\left({i}\right) \\ $$$$\mathrm{cos}\:\alpha=\frac{{a}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} }{\mathrm{2}{as}} \\ $$$$\mathrm{cos}\:\beta=\frac{{a}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }{\mathrm{2}{as}}=\mathrm{sin}\:\alpha \\ $$$$\left(\frac{{a}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{100}}{\mathrm{2}{as}}\right)^{\mathrm{2}} +\left(\frac{{a}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{16}}{\mathrm{2}{as}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\left({a}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{100}\right)^{\mathrm{2}} +\left({a}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{16}\right)^{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} {s}^{\mathrm{2}} \\ $$$${a}^{\mathrm{4}} +{s}^{\mathrm{4}} −\mathrm{116}\left({a}^{\mathrm{2}} +{s}^{\mathrm{2}} \right)+\mathrm{5128}=\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$${from}\:\left({i}\right): \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{39}\left({s}^{\mathrm{2}} −\mathrm{442}\right)}{\mathrm{44}}+\mathrm{394}=\frac{\mathrm{39}{s}^{\mathrm{2}} }{\mathrm{44}}+\frac{\mathrm{49}}{\mathrm{22}} \\ $$$${put}\:{this}\:{into}\:\left({ii}\right): \\ $$$$\left(\frac{\mathrm{39}{s}^{\mathrm{2}} }{\mathrm{44}}+\frac{\mathrm{49}}{\mathrm{22}}\right)^{\mathrm{2}} +{s}^{\mathrm{4}} −\mathrm{116}\left(\frac{\mathrm{39}{s}^{\mathrm{2}} }{\mathrm{44}}+\frac{\mathrm{49}}{\mathrm{22}}+{s}^{\mathrm{2}} \right)+\mathrm{5128}=\mathrm{0} \\ $$$$\frac{\mathrm{3457}}{\mathrm{4}}{s}^{\mathrm{4}} −\mathrm{103997}{s}^{\mathrm{2}} +\mathrm{2359305}=\mathrm{0} \\ $$$${S}={s}^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{103997}\pm\mathrm{51568}}{\mathrm{3457}}\right)=\mathrm{90}\:{or}\:\mathrm{30}\frac{\mathrm{1148}}{\mathrm{3457}} \\ $$
