
Question Number 131637 by rs4089 last updated on 07/Feb/21
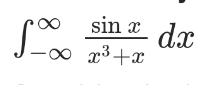
Answered by Dwaipayan Shikari last updated on 07/Feb/21
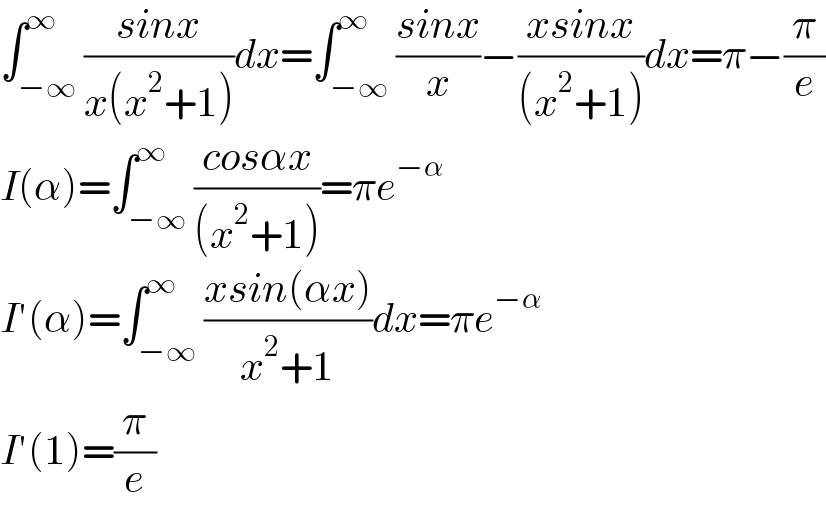
$$\int_{−\infty} ^{\infty} \frac{{sinx}}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}=\int_{−\infty} ^{\infty} \frac{{sinx}}{{x}}−\frac{{xsinx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}=\pi−\frac{\pi}{{e}} \\ $$$${I}\left(\alpha\right)=\int_{−\infty} ^{\infty} \frac{{cos}\alpha{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)}=\pi{e}^{−\alpha} \\ $$$${I}'\left(\alpha\right)=\int_{−\infty} ^{\infty} \frac{{xsin}\left(\alpha{x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\pi{e}^{−\alpha} \\ $$$${I}'\left(\mathrm{1}\right)=\frac{\pi}{{e}} \\ $$
Commented by Lordose last updated on 07/Feb/21
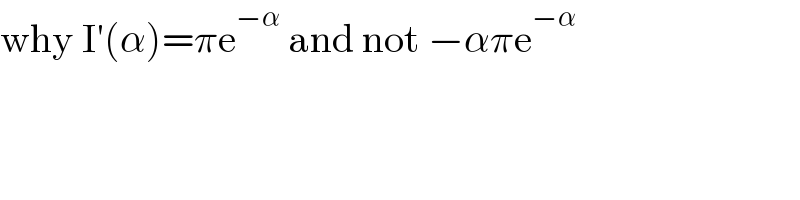
$$\mathrm{why}\:\mathrm{I}'\left(\alpha\right)=\pi\mathrm{e}^{−\alpha} \:\mathrm{and}\:\mathrm{not}\:−\alpha\pi\mathrm{e}^{−\alpha} \\ $$
Commented by Dwaipayan Shikari last updated on 07/Feb/21
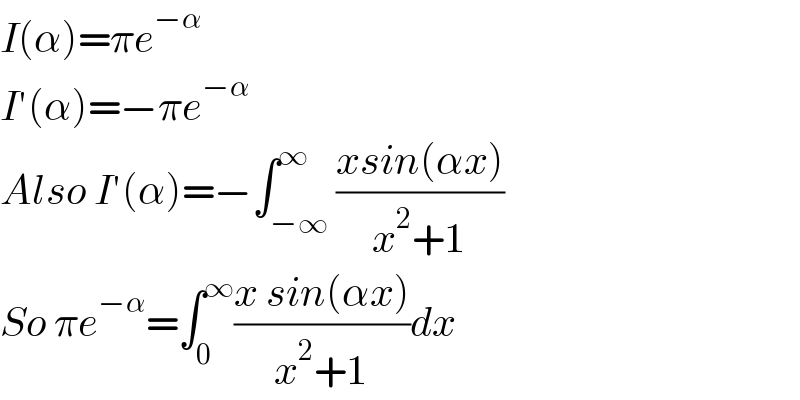
$${I}\left(\alpha\right)=\pi{e}^{−\alpha} \\ $$$${I}'\left(\alpha\right)=−\pi{e}^{−\alpha} \\ $$$${Also}\:{I}'\left(\alpha\right)=−\int_{−\infty} ^{\infty} \frac{{xsin}\left(\alpha{x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${So}\:\pi{e}^{−\alpha} =\int_{\mathrm{0}} ^{\infty} \frac{{x}\:{sin}\left(\alpha{x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$
Answered by mathmax by abdo last updated on 07/Feb/21
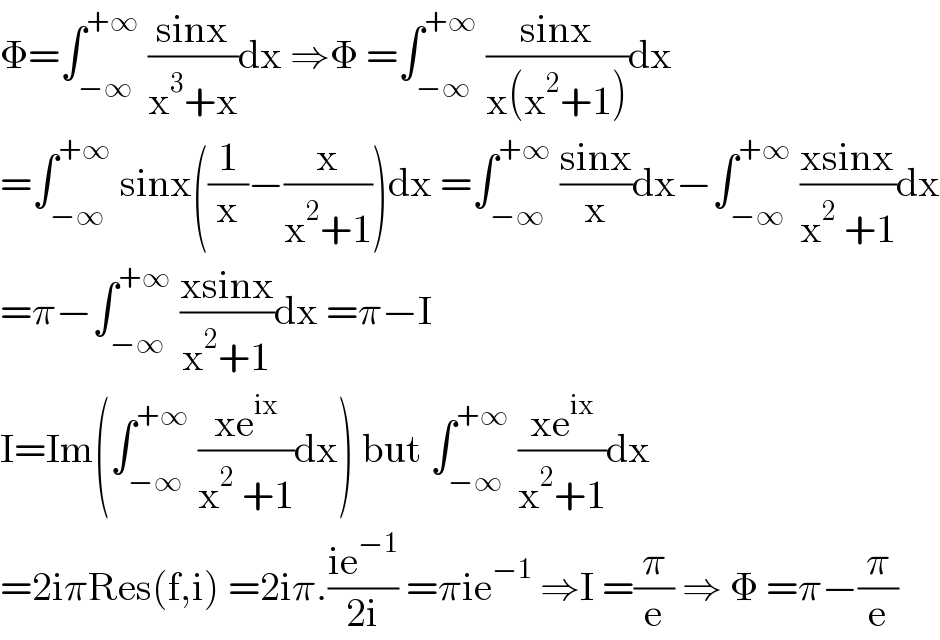
$$\Phi=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{sinx}}{\mathrm{x}^{\mathrm{3}} +\mathrm{x}}\mathrm{dx}\:\Rightarrow\Phi\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{sinx}}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \:\mathrm{sinx}\left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)\mathrm{dx}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{sinx}}{\mathrm{x}}\mathrm{dx}−\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xsinx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx} \\ $$$$=\pi−\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xsinx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:=\pi−\mathrm{I} \\ $$$$\mathrm{I}=\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xe}^{\mathrm{ix}} }{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\right)\:\mathrm{but}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xe}^{\mathrm{ix}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$=\mathrm{2i}\pi\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)\:=\mathrm{2i}\pi.\frac{\mathrm{ie}^{−\mathrm{1}} }{\mathrm{2i}}\:=\pi\mathrm{ie}^{−\mathrm{1}} \:\Rightarrow\mathrm{I}\:=\frac{\pi}{\mathrm{e}}\:\Rightarrow\:\Phi\:=\pi−\frac{\pi}{\mathrm{e}} \\ $$
