
Question Number 131584 by mr W last updated on 06/Feb/21
Commented by mr W last updated on 06/Feb/21

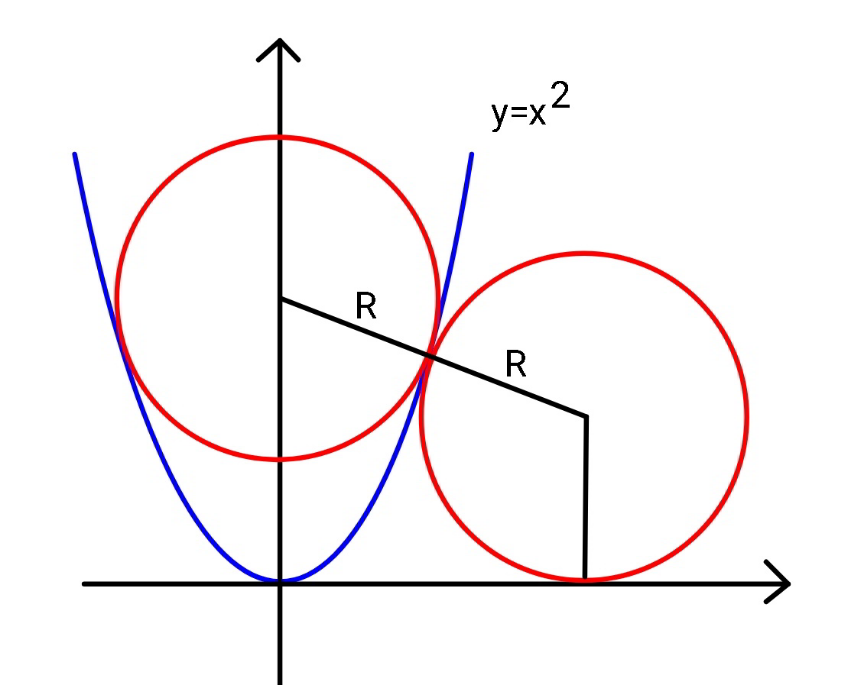
$${find}\:{R}=? \\ $$
Answered by ajfour last updated on 06/Feb/21
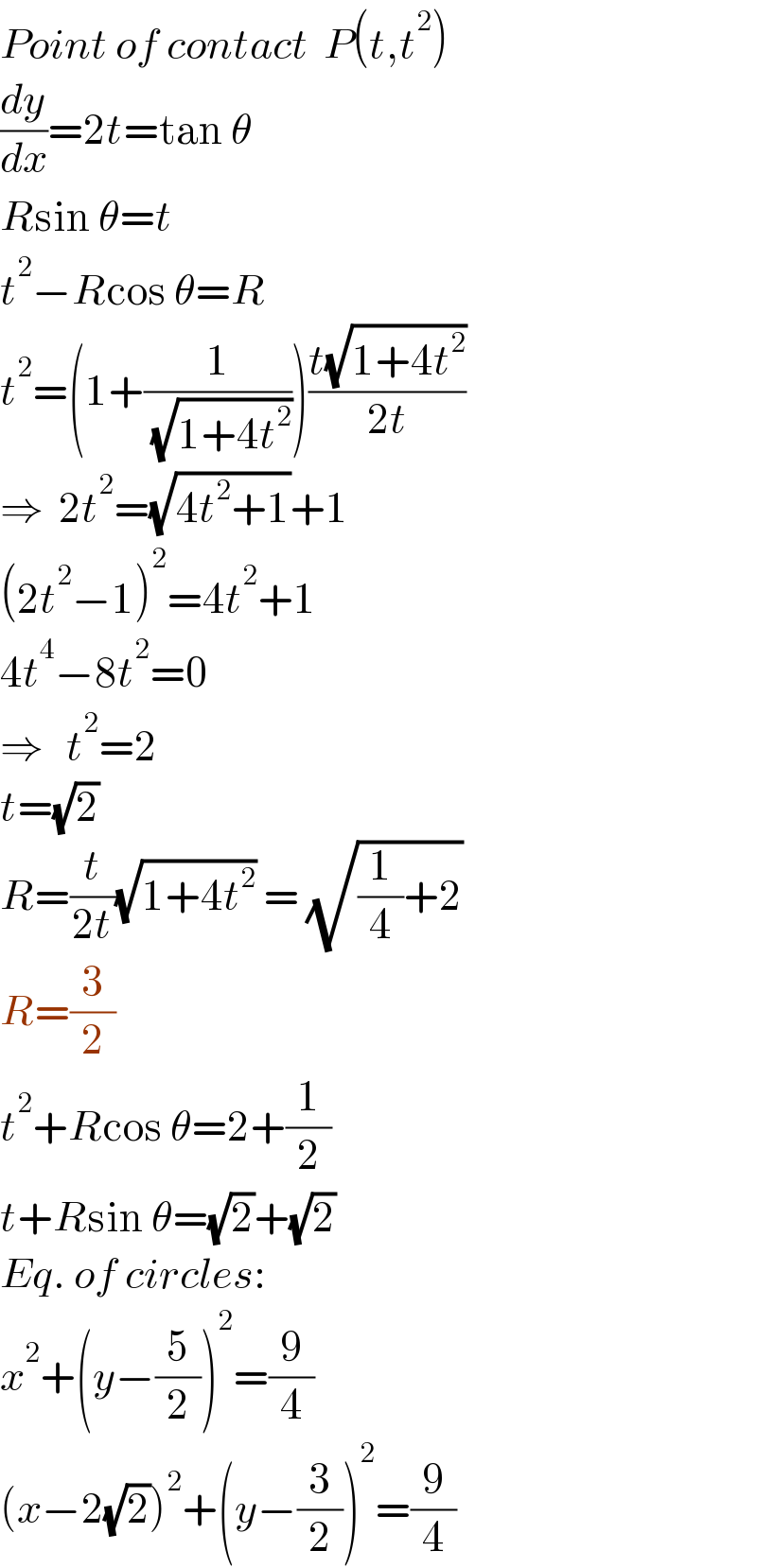
$${Point}\:{of}\:{contact}\:\:{P}\left({t},{t}^{\mathrm{2}} \right) \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2}{t}=\mathrm{tan}\:\theta \\ $$$${R}\mathrm{sin}\:\theta={t} \\ $$$${t}^{\mathrm{2}} −{R}\mathrm{cos}\:\theta={R} \\ $$$${t}^{\mathrm{2}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}\right)\frac{{t}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }}{\mathrm{2}{t}} \\ $$$$\Rightarrow\:\:\mathrm{2}{t}^{\mathrm{2}} =\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}+\mathrm{1} \\ $$$$\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{4}{t}^{\mathrm{4}} −\mathrm{8}{t}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:\:{t}^{\mathrm{2}} =\mathrm{2} \\ $$$${t}=\sqrt{\mathrm{2}}\:\:\: \\ $$$${R}=\frac{{t}}{\mathrm{2}{t}}\sqrt{\mathrm{1}+\mathrm{4}{t}^{\mathrm{2}} }\:=\:\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{2}} \\ $$$${R}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${t}^{\mathrm{2}} +{R}\mathrm{cos}\:\theta=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${t}+{R}\mathrm{sin}\:\theta=\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}} \\ $$$${Eq}.\:{of}\:{circles}: \\ $$$${x}^{\mathrm{2}} +\left({y}−\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\left({x}−\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{4}} \\ $$
Commented by ajfour last updated on 06/Feb/21
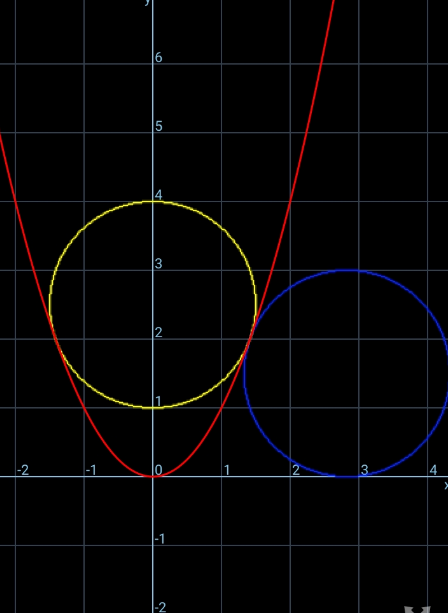
Commented by mr W last updated on 06/Feb/21

$${thanks}\:{sir}! \\ $$
