Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 131420 by ajfour last updated on 04/Feb/21

Commented by ajfour last updated on 04/Feb/21

In terms of ellipse parameters a and b, find radius of the equal radii circles.

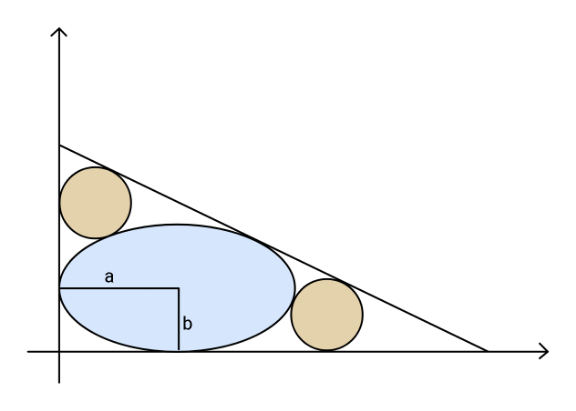
$${In}\:{terms}\:{of}\:{ellipse}\:{parameters} \\ $$$${a}\:{and}\:{b},\:{find}\:{radius}\:{of}\:{the} \\ $$$${equal}\:{radii}\:{circles}. \\ $$

Answered by mr W last updated on 04/Feb/21

Commented by mr W last updated on 05/Feb/21

let μ=(b/a) say P(a+a cos φ, b+b sin φ) tan θ=(b/(a tan φ))=(μ/(tan φ)) tan φ=(μ/(tan θ)) sin φ=(μ/( (√(μ^2 +tan^2 θ)))) cos φ=((tan θ)/( (√(μ^2 +tan^2 θ)))) y=b+b sin φ−(μ/(tan φ)) (x−a−a cos φ) 0=b(1+sin φ)−(μ/(tan φ)) (x_A −a(1+cos φ)) (1+sin φ)=(1/(tan φ)) ((x_A /a)−(1+cos φ)) ⇒(x_A /a)=1+cos φ+(1+sin φ)tan φ ⇒(x_A /a)=1+((tan θ)/( (√(μ^2 +tan^2 θ))))+(1+(μ/( (√(μ^2 +tan^2 θ)))))(μ/(tan θ)) ⇒(x_A /a)=1+(μ/(tan θ))+(√(1+((μ/(tan θ)))^2 )) say Q(a+a cos α, b−b sin α) tan ϕ=(μ/(tan α)) tan α=(μ/(tan ϕ)) sin α=(μ/( (√(μ^2 +tan^2 ϕ)))) cos α=((tan ϕ)/( (√(μ^2 +tan^2 ϕ)))) x_C =a+a cos α+r sin ϕ=x_A −(r/(tan (θ/2))) 1+cos α+λ sin ϕ=1+(μ/(tan θ))+(√(1+((μ/(tan θ)))^2 ))−(λ/(tan (θ/2))) let λ=(r/a) ((tan ϕ)/( (√(μ^2 +tan^2 ϕ))))+λ(sin ϕ+(1/(tan (θ/2))))=(μ/(tan θ))+(√(1+((μ/(tan θ)))^2 )) y_C =b−b sin α−r cos ϕ=r μ(1−sin α)=λ(1+cos ϕ) λ=(r/a)=(μ/(1+cos ϕ))(1−(μ/( (√(μ^2 +tan^2 ϕ))))) ((tan ϕ)/( (√(μ^2 +tan^2 ϕ))))+(μ/(1+cos ϕ))(1−(μ/( (√(μ^2 +tan^2 ϕ)))))(sin ϕ+(1/(tan (θ/2))))=(μ/(tan θ))+(√(1+((μ/(tan θ)))^2 )) ...(I) similarly (r/b)=(1/(μ(1+cos δ)))(1−(1/( (√(1+μ^2 tan^2 δ))))) ((μ tan δ)/( (√(1+μ^2 tan^2 δ))))+(1/(μ(1+cos δ)))(1−(1/( (√(1+μ^2 tan^2 δ)))))(sin δ+(1/(tan ((π/4)−(θ/2)))))=((tan θ)/μ)+(√(1+(((tan θ)/μ))^2 )) ...(II) (1/(μ(1+cos δ)))(1−(1/( (√(1+μ^2 tan^2 δ)))))=(1/(1+cos ϕ))(1−(μ/( (√(μ^2 +tan^2 ϕ))))) ...(III) three eqn. for three unknowns: θ,ϕ,δ. ......

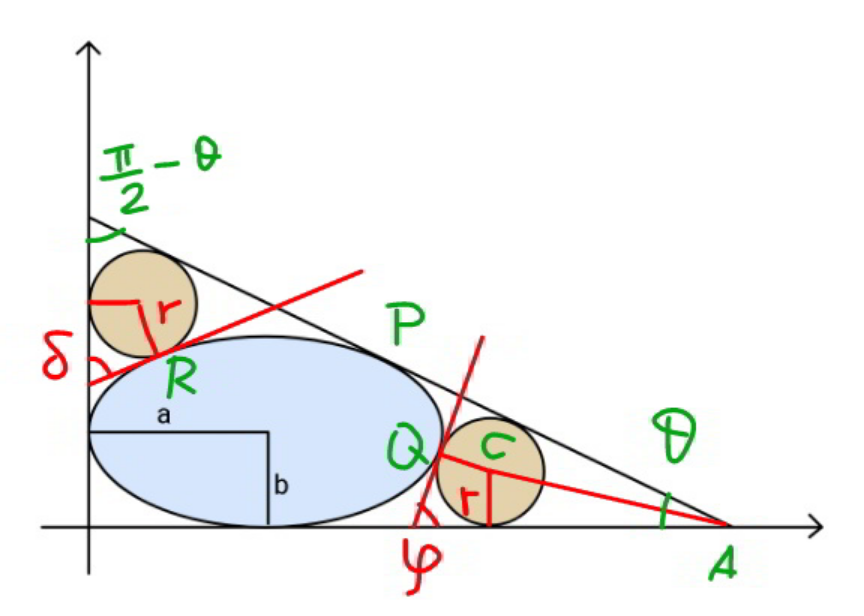
$${let}\:\mu=\frac{{b}}{{a}} \\ $$$${say}\:{P}\left({a}+{a}\:\mathrm{cos}\:\phi,\:{b}+{b}\:\mathrm{sin}\:\phi\right) \\ $$$$\mathrm{tan}\:\theta=\frac{{b}}{{a}\:\mathrm{tan}\:\phi}=\frac{\mu}{\mathrm{tan}\:\phi} \\ $$$$\mathrm{tan}\:\phi=\frac{\mu}{\mathrm{tan}\:\theta} \\ $$$$\mathrm{sin}\:\phi=\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}} \\ $$$$\mathrm{cos}\:\phi=\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}} \\ $$$${y}={b}+{b}\:\mathrm{sin}\:\phi−\frac{\mu}{\mathrm{tan}\:\phi}\:\left({x}−{a}−{a}\:\mathrm{cos}\:\phi\right) \\ $$$$\mathrm{0}={b}\left(\mathrm{1}+\mathrm{sin}\:\phi\right)−\frac{\mu}{\mathrm{tan}\:\phi}\:\left({x}_{{A}} −{a}\left(\mathrm{1}+\mathrm{cos}\:\phi\right)\right) \\ $$$$\left(\mathrm{1}+\mathrm{sin}\:\phi\right)=\frac{\mathrm{1}}{\mathrm{tan}\:\phi}\:\left(\frac{{x}_{{A}} }{{a}}−\left(\mathrm{1}+\mathrm{cos}\:\phi\right)\right) \\ $$$$\Rightarrow\frac{{x}_{{A}} }{{a}}=\mathrm{1}+\mathrm{cos}\:\phi+\left(\mathrm{1}+\mathrm{sin}\:\phi\right)\mathrm{tan}\:\phi \\ $$$$\Rightarrow\frac{{x}_{{A}} }{{a}}=\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}+\left(\mathrm{1}+\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}\right)\frac{\mu}{\mathrm{tan}\:\theta} \\ $$$$\Rightarrow\frac{{x}_{{A}} }{{a}}=\mathrm{1}+\frac{\mu}{\mathrm{tan}\:\theta}+\sqrt{\mathrm{1}+\left(\frac{\mu}{\mathrm{tan}\:\theta}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${say}\:{Q}\left({a}+{a}\:\mathrm{cos}\:\alpha,\:{b}−{b}\:\mathrm{sin}\:\alpha\right) \\ $$$$\mathrm{tan}\:\varphi=\frac{\mu}{\mathrm{tan}\:\alpha} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mu}{\mathrm{tan}\:\varphi} \\ $$$$\mathrm{sin}\:\alpha=\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\varphi}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{tan}\:\varphi}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\varphi}} \\ $$$${x}_{{C}} ={a}+{a}\:\mathrm{cos}\:\alpha+{r}\:\mathrm{sin}\:\varphi={x}_{{A}} −\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\mathrm{1}+\mathrm{cos}\:\alpha+\lambda\:\mathrm{sin}\:\varphi=\mathrm{1}+\frac{\mu}{\mathrm{tan}\:\theta}+\sqrt{\mathrm{1}+\left(\frac{\mu}{\mathrm{tan}\:\theta}\right)^{\mathrm{2}} }−\frac{\lambda}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$${let}\:\lambda=\frac{{r}}{{a}} \\ $$$$\frac{\mathrm{tan}\:\varphi}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\varphi}}+\lambda\left(\mathrm{sin}\:\varphi+\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}\right)=\frac{\mu}{\mathrm{tan}\:\theta}+\sqrt{\mathrm{1}+\left(\frac{\mu}{\mathrm{tan}\:\theta}\right)^{\mathrm{2}} } \\ $$$${y}_{{C}} ={b}−{b}\:\mathrm{sin}\:\alpha−{r}\:\mathrm{cos}\:\varphi={r} \\ $$$$\mu\left(\mathrm{1}−\mathrm{sin}\:\alpha\right)=\lambda\left(\mathrm{1}+\mathrm{cos}\:\varphi\right) \\ $$$$\lambda=\frac{{r}}{{a}}=\frac{\mu}{\mathrm{1}+\mathrm{cos}\:\varphi}\left(\mathrm{1}−\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\varphi}}\right) \\ $$$$\frac{\mathrm{tan}\:\varphi}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\varphi}}+\frac{\mu}{\mathrm{1}+\mathrm{cos}\:\varphi}\left(\mathrm{1}−\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\varphi}}\right)\left(\mathrm{sin}\:\varphi+\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}\right)=\frac{\mu}{\mathrm{tan}\:\theta}+\sqrt{\mathrm{1}+\left(\frac{\mu}{\mathrm{tan}\:\theta}\right)^{\mathrm{2}} }\:\:\:...\left({I}\right) \\ $$$${similarly} \\ $$$$\frac{{r}}{{b}}=\frac{\mathrm{1}}{\mu\left(\mathrm{1}+\mathrm{cos}\:\delta\right)}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mu^{\mathrm{2}} \:\mathrm{tan}^{\mathrm{2}} \:\delta}}\right) \\ $$$$\frac{\mu\:\mathrm{tan}\:\delta}{\:\sqrt{\mathrm{1}+\mu^{\mathrm{2}} \:\mathrm{tan}^{\mathrm{2}} \:\delta}}+\frac{\mathrm{1}}{\mu\left(\mathrm{1}+\mathrm{cos}\:\delta\right)}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mu^{\mathrm{2}} \:\mathrm{tan}^{\mathrm{2}} \:\delta}}\right)\left(\mathrm{sin}\:\delta+\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)}\right)=\frac{\mathrm{tan}\:\theta}{\mu}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{tan}\:\theta}{\mu}\right)^{\mathrm{2}} }\:\:\:...\left({II}\right) \\ $$$$\frac{\mathrm{1}}{\mu\left(\mathrm{1}+\mathrm{cos}\:\delta\right)}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mu^{\mathrm{2}} \:\mathrm{tan}^{\mathrm{2}} \:\delta}}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\varphi}\left(\mathrm{1}−\frac{\mu}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\varphi}}\right)\:\:\:...\left({III}\right) \\ $$$${three}\:{eqn}.\:{for}\:{three}\:{unknowns}:\:\theta,\varphi,\delta. \\ $$$$...... \\ $$

Answered by ajfour last updated on 04/Feb/21

Commented by mr W last updated on 05/Feb/21

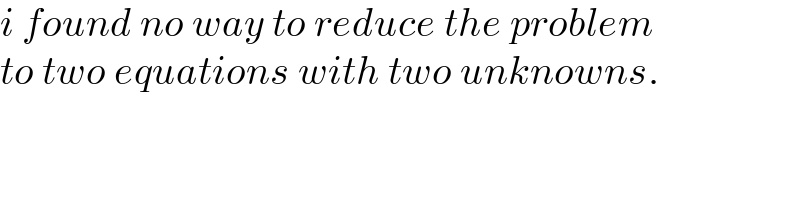
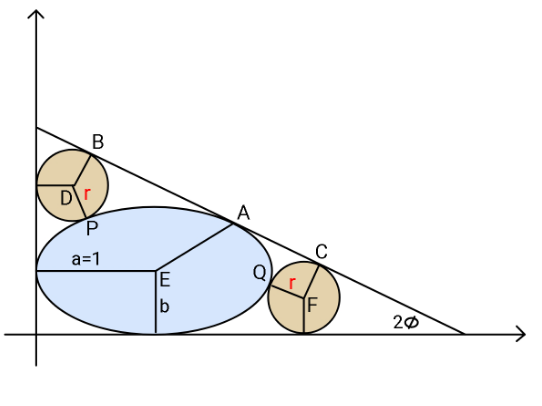
i found no way to reduce the problem to two equations with two unknowns.

$${i}\:{found}\:{no}\:{way}\:{to}\:{reduce}\:{the}\:{problem} \\ $$$${to}\:{two}\:{equations}\:{with}\:{two}\:{unknowns}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com