
Question Number 130965 by Hilolaxon last updated on 31/Jan/21
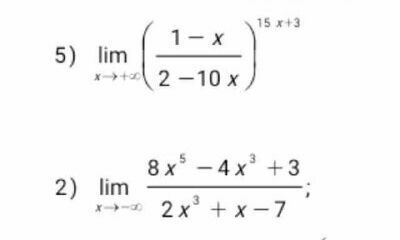
Answered by bramlexs22 last updated on 31/Jan/21
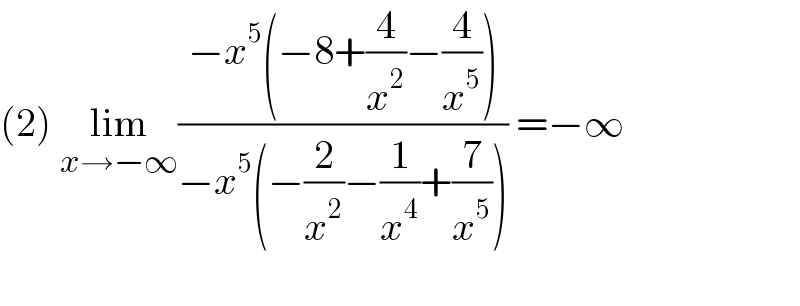
$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{−{x}^{\mathrm{5}} \left(−\mathrm{8}+\frac{\mathrm{4}}{{x}^{\mathrm{2}} }−\frac{\mathrm{4}}{{x}^{\mathrm{5}} }\right)}{−{x}^{\mathrm{5}} \left(−\frac{\mathrm{2}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{\mathrm{7}}{{x}^{\mathrm{5}} }\right)}\:=−\infty\: \\ $$$$\:\:\:\:\: \\ $$
Answered by bramlexs22 last updated on 31/Jan/21
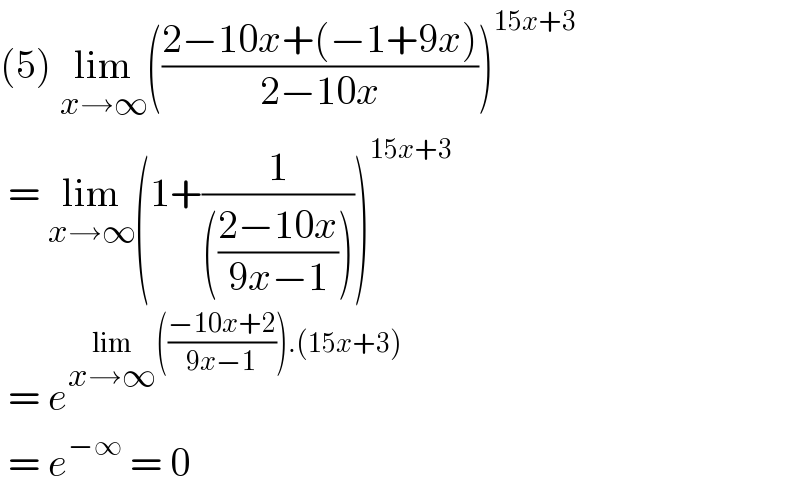
$$\left(\mathrm{5}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}−\mathrm{10}{x}+\left(−\mathrm{1}+\mathrm{9}{x}\right)}{\mathrm{2}−\mathrm{10}{x}}\right)^{\mathrm{15}{x}+\mathrm{3}} \\ $$$$\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{\left(\frac{\mathrm{2}−\mathrm{10}{x}}{\mathrm{9}{x}−\mathrm{1}}\right)}\right)^{\mathrm{15}{x}+\mathrm{3}} \\ $$$$\:=\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{−\mathrm{10}{x}+\mathrm{2}}{\mathrm{9}{x}−\mathrm{1}}\right).\left(\mathrm{15}{x}+\mathrm{3}\right)} \\ $$$$\:=\:{e}^{−\infty} \:=\:\mathrm{0} \\ $$
Answered by greg_ed last updated on 31/Jan/21
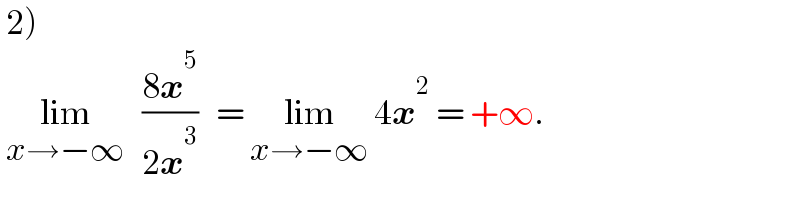
$$\left.\:\mathrm{2}\right)\: \\ $$$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\:\:\frac{\mathrm{8}\boldsymbol{{x}}^{\mathrm{5}} }{\mathrm{2}\boldsymbol{{x}}^{\mathrm{3}} }\:\:\:=\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} \:=\:+\infty. \\ $$
Answered by JDamian last updated on 31/Jan/21
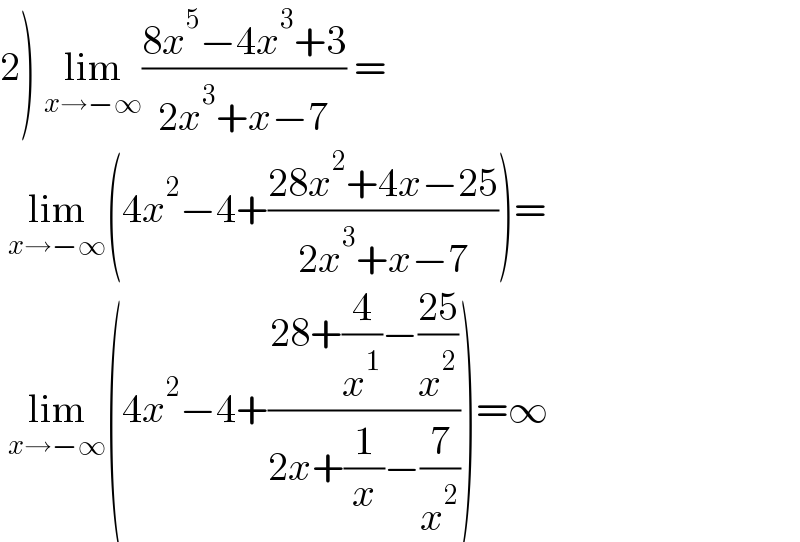
$$\left.\mathrm{2}\right)\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\mathrm{8}{x}^{\mathrm{5}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{3}}{\mathrm{2}{x}^{\mathrm{3}} +{x}−\mathrm{7}}\:=\: \\ $$$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}+\frac{\mathrm{28}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{25}}{\mathrm{2}{x}^{\mathrm{3}} +{x}−\mathrm{7}}\right)= \\ $$$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}+\frac{\mathrm{28}+\frac{\mathrm{4}}{{x}^{\mathrm{1}} }−\frac{\mathrm{25}}{{x}^{\mathrm{2}} }}{\mathrm{2}{x}+\frac{\mathrm{1}}{{x}}−\frac{\mathrm{7}}{{x}^{\mathrm{2}} }}\right)=\infty \\ $$
Answered by mathmax by abdo last updated on 31/Jan/21
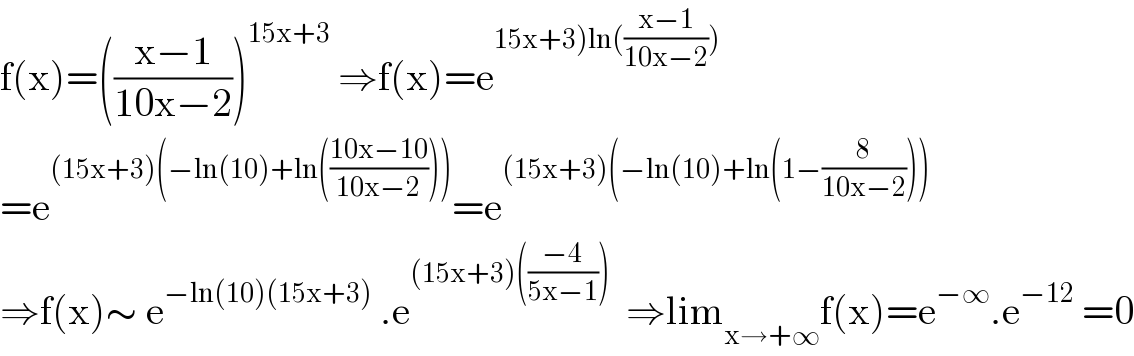
$$\mathrm{f}\left(\mathrm{x}\right)=\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{10x}−\mathrm{2}}\right)^{\mathrm{15x}+\mathrm{3}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\left.\mathrm{15x}+\mathrm{3}\right)\mathrm{ln}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{10x}−\mathrm{2}}\right)} \\ $$$$=\mathrm{e}^{\left(\mathrm{15x}+\mathrm{3}\right)\left(−\mathrm{ln}\left(\mathrm{10}\right)+\mathrm{ln}\left(\frac{\mathrm{10x}−\mathrm{10}}{\mathrm{10x}−\mathrm{2}}\right)\right)} =\mathrm{e}^{\left(\mathrm{15x}+\mathrm{3}\right)\left(−\mathrm{ln}\left(\mathrm{10}\right)+\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{8}}{\mathrm{10x}−\mathrm{2}}\right)\right)} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\:\mathrm{e}^{−\mathrm{ln}\left(\mathrm{10}\right)\left(\mathrm{15x}+\mathrm{3}\right)} \:.\mathrm{e}^{\left(\mathrm{15x}+\mathrm{3}\right)\left(\frac{−\mathrm{4}}{\mathrm{5x}−\mathrm{1}}\right)} \:\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{−\infty} .\mathrm{e}^{−\mathrm{12}} \:=\mathrm{0} \\ $$
