
Question Number 130876 by 0731619177 last updated on 30/Jan/21

Answered by Dwaipayan Shikari last updated on 30/Jan/21
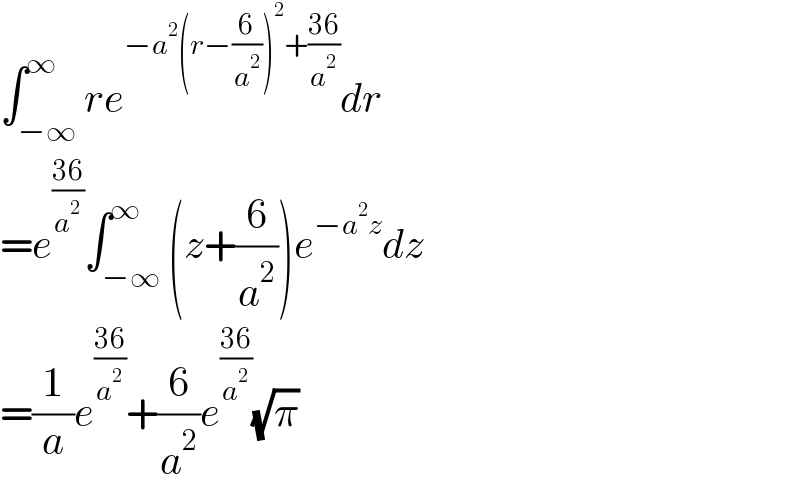
$$\int_{−\infty} ^{\infty} {re}^{−{a}^{\mathrm{2}} \left({r}−\frac{\mathrm{6}}{{a}^{\mathrm{2}} }\right)^{\mathrm{2}} +\frac{\mathrm{36}}{{a}^{\mathrm{2}} }} {dr} \\ $$$$={e}^{\frac{\mathrm{36}}{{a}^{\mathrm{2}} }} \int_{−\infty} ^{\infty} \left({z}+\frac{\mathrm{6}}{{a}^{\mathrm{2}} }\right){e}^{−{a}^{\mathrm{2}} {z}} {dz} \\ $$$$=\frac{\mathrm{1}}{{a}}{e}^{\frac{\mathrm{36}}{{a}^{\mathrm{2}} }} +\frac{\mathrm{6}}{{a}^{\mathrm{2}} }{e}^{\frac{\mathrm{36}}{{a}^{\mathrm{2}} }} \sqrt{\pi} \\ $$
